Intuition behind Matrix Multiplication

Solution 1:

Matrix ¨multiplication¨ is the composition of two linear functions. The composition of two linear functions is a linear function.

If a linear function is represented by A and another by B then AB is their composition. BA is the their reverse composition.

Thats one way of thinking of it. It explains why matrix multiplication is the way it is instead of piecewise multiplication.

Solution 2:

Asking why matrix multiplication isn't just componentwise multiplication is an excellent question: in fact, componentwise multiplication is in some sense the most "natural" generalization of real multiplication to matrices: it satisfies all of the axioms you would expect (associativity, commutativity, existence of identity and inverses (for matrices with no 0 entries), distributivity over addition).

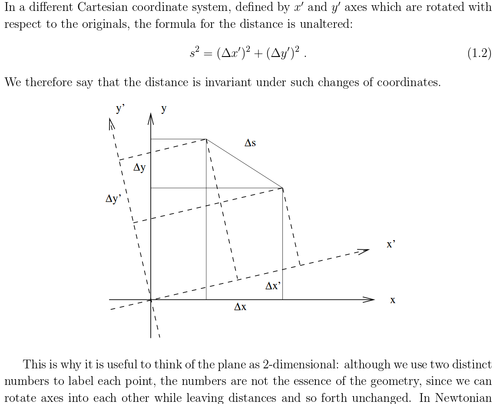
The usual matrix multiplication in fact "gives up" commutativity; we all know that in general $AB \neq BA$ while for real numbers $ab = ba$. What do we gain? Invariance with respect to change of basis. If $P$ is an invertible matrix,

$$P^{-1}AP + P^{-1}BP = P^{-1}(A+B)P$$ $$(P^{-1}AP) (P^{-1}BP) = P^{-1}(AB)P$$ In other words, it doesn't matter what basis you use to represent the matrices $A$ and $B$, no matter what choice you make their sum and product is the same.

It is easy to see by trying an example that the second property does not hold for multiplication defined component-wise. This is because the inverse of a change of basis $P^{-1}$ no longer corresponds to the multiplicative inverse of $P$.

Solution 3:

The short answer is that a matrix corresponds to a linear transformation. To multiply two matrices is the same thing as composing the corresponding linear transformations (or linear maps).

The following is covered in a text on linear algebra (such as Hoffman-Kunze):

This makes most sense in the context of vector spaces over a field. You can talk about vector spaces and (linear) maps between them without ever mentioning a basis. When you pick a basis, you can write the elements of your vector space as a sum of basis elements with coefficients in your base field (that is, you get explicit coordinates for your vectors in terms of for instance real numbers). If you want to compute something, you typically pick bases for your vector spaces. Then you can represent your linear map as a matrix with respect to the given bases, with entries in your base field (see e.g. the above mentioned book for details as to how). We define matrix multiplication such that matrix multiplication corresponds to composition of the linear maps.

Added (Details on the presentation of a linear map by a matrix). Let $V$ and $W$ be two vector spaces with ordered bases $e_1,\dots,e_n$ and $f_1,\dots,f_m$ respectively, and $L:V\to W$ a linear map.

First note that since the $e_j$ generate $V$ and $L$ is linear, $L$ is completely determined by the images of the $e_j$ in $W$, that is, $L(e_j)$. Explicitly, note that by the definition of a basis any $v\in V$ has a unique expression of the form $a_1e_1+\cdots+a_ne_n$, and $L$ applied to this pans out as $a_1L(e_1)+\cdots+a_nL(e_n)$.

Now, since $L(e_j)$ is in $W$ it has a unique expression of the form $b_1f_1+\dots+b_mf_m$, and it is clear that the value of $e_j$ under $L$ is uniquely determined by $b_1,\dots,b_m$, the coefficients of $L(e_j)$ with respect to the given ordered basis for $W$. In order to keep track of which $L(e_j)$ the $b_i$ are meant to represent, we write (abusing notation for a moment) $m_{ij}=b_i$, yielding the matrix $(m_{ij})$ of $L$ with respect to the given ordered bases.

This might be enough to play around with why matrix multiplication is defined the way it is. Try for instance a single vector space $V$ with basis $e_1,\dots,e_n$, and compute the corresponding matrix of the square $L^2=L\circ L$ of a single linear transformation $L:V\to V$, or say, compute the matrix corresponding to the identity transformation $v\mapsto v$.

Solution 4:

By Flanigan & Kazdan:

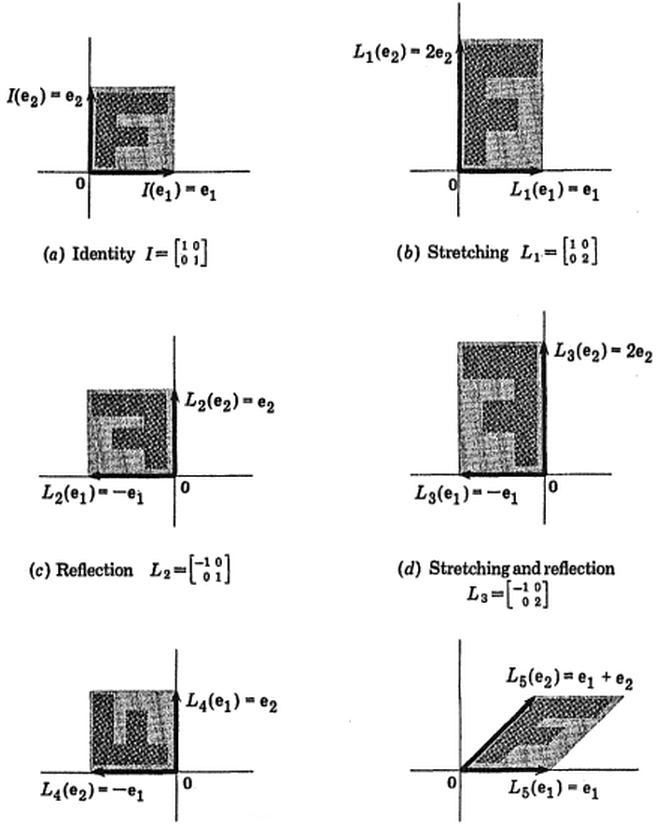
Instead of looking at a "box of numbers", look at the "total action" after applying the whole thing. It's an automorphism of linear spaces, meaning that in some vector-linear-algebra-type situation this is "turning things over and over in your hands without breaking the algebra that makes it be what it is". (Modulo some things—like maybe you want a constant determinant.)

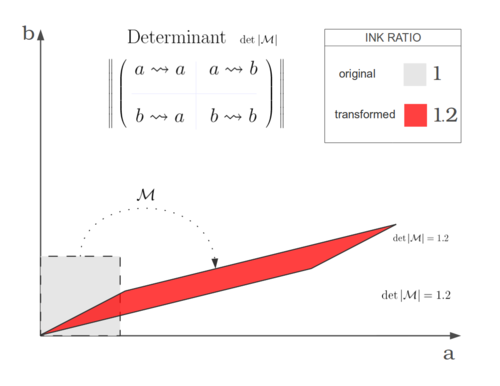
This is also why order matters: if you compose the matrices in one direction it might not be the same as the other. $$^1_4 \Box ^2_3 {} \xrightarrow{\mathbf{V} \updownarrow} {} ^4_1 \Box ^3_2 {} \xrightarrow{\Theta_{90} \curvearrowright} {} ^1_2 \Box ^4_3 $$ versus $$^1_4 \Box ^2_3 {} \xrightarrow{\Theta_{90} \curvearrowright} {} ^4_3 \Box ^1_2 {} \xrightarrow{\mathbf{V} \updownarrow} {} ^3_4 \Box ^2_1 $$

The actions can be composed (one after the other)—that's what multiplying matrices does. Eventually the matrix representing the overall cumulative effect of whatever things you composed, should be applied to something. For this you can say "the plane", or pick a few points, or draw an F, or use a real picture (computers are good at linear transformations after all).

You could also watch the matrices work on Mona step by step too, to help your intuition.

Finally I think you can think of matrices as "multidimensional multiplication". $$y=mx+b$$ is affine; the truly "linear" (keeping $0 \overset{f}{\longmapsto} 0$) would be less complicated: just $$y=mx$$ (eg. ) which is an "even" stretching/dilation. $$\vec{y}=\left[ \mathbf{M} \right] \vec{x}$$ really is the multi-dimensional version of the same thing, it's just that when you have multiple numbers in each $\vec{x}$ each of the dimensions can impinge on each other for example in the case of a rotation—in physics it doesn't matter which orthonormal coördinate system you choose, so we want to "quotient away" that invariant our physical theories.