How does $e^{\pi i}$ equal $-1$

I was on xkcd a while back and there was the equation $e^{\pi i}$ which somehow miraculously equals $-1$. So, I put it into Google and it works. So, I tried solving it on my own:

$\begin{align} e^{\pi i} &= -1 \\ \ln e^{\pi i} &= \ln (-1) \\ \pi i \times \ln e &= \ln (-1) \\ \pi i \times 1 &= \ln (-1) \\ \pi i &= \ln (-1) \end{align}$

But that's as far as I can get as $\ln (-1)$ gives Error on my calculator. So how does $e^{\pi i} = -1$ work?

Solution 1:

This is an interesting proof that you may have seen.

Let us define

$$e^x := \sum_{n=0}^\infty \frac{x^n}{n!}$$

Then \begin{align}e^{i \pi} &= \sum_{n=0}^\infty \frac{(i\pi)^n}{n!} \\ &= 1+i\pi-\frac{\pi^2}{2}-\frac{\pi^3}{3!} + \cdots\\ &= \left(1-\frac{\pi^2}{2}+\frac{\pi^4}{4!}+\cdots\right) + i\left(\pi-\frac{\pi^3}{3!}+\frac{\pi^5}{5!}+\cdots\right) \\ \\ &= \cos \pi +i\sin \pi \\ \\ &= -1\end{align}

This method can be generalized to show Euler's identity, $e^{i\theta}=\cos \theta+i\sin\theta$. From this we find that $e^z$ is actually a periodic function over $2\pi i$, and because of this, it follows that $\log z$, as the inverse of $e^z$, must be multivalued (because, $e^{i\theta} = e^{i\theta +2\pi i}=e^{i\theta -2\pi i}=\cdots = e^{i\theta+2 \pi i n}$ where $n \in \mathbb Z$).

Solution 2:

$e^{\pi i}$ corresponds to $z = (-1, 0) = -1$ on the unit circle in the complex plane.

That is, it is positioned $\pi = 180^\circ$ from the position (1, 0) on the complex unit circle. It has no "height" in the direction of either $i$ or $-i$.

From $e^{\pi i} = -1$, we obtain Euler's Identity: $e^{\pi i} + 1 = 0$.

Indeed one of the amazing things is that $e$ and $\pi$ have a lot to do with each other:

For example, see Euler's formula: $\quad e^{i\theta} = \cos \theta + i\sin \theta$.

So $e^{\pi i} = \cos {\pi} + i \sin {\pi} = -1 + (i \times 0)$.

A visual image may help make sense of Euler's formula and $e^{\pi i}$:

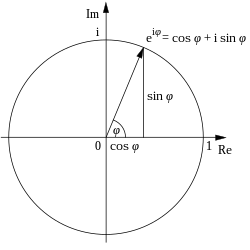
If you really want to pursue this question, and how Euler came up with his formula, you may want take on the following challenge:

Try computing the Taylor expansion (Maclaurin Series) of $e^{\pi i}$ and see that it equals sum of the Taylor (Maclaurin) expansions of $\cos {\pi}$ and $i \sin {\pi}$. Both sum to $-1$! Or if you are lazy, you can look over at Wikipedia

BOTH $e$ and $i$ are fascinating, because they "crop up" almost everywhere in math, physics, and many other fields. For more ways of representing $e$, look at this list.

Solution 3:

First you need to understand why, for a complex number $z$, $z = x + iy$ and $z = r e^{i \theta}$ -- where $x = r \cos \theta$ and $y = r \sin \theta$ -- are equivalent. From that, $e^{\pi i\left(1+2n\right)} = -1$ and $\ln \left(-1\right) = \pi i \left(1 + 2 n\right)$ follow for $n$ integer.

To see the former, substitute $r=1$ and $\theta = \pi\left(1+2n\right)$ into $r e^{i \theta} = r \cos \theta + i r \sin \theta$.

To see the latter, take $\ln$ of the result $e^{\pi i\left(1+2n\right)} = -1$, or take $\ln$ of $z = e^{i \theta}$: $$ \ln z = \ln r e^{i \theta} = \ln r + i \theta. $$ With $z = -1$, $r = 1$ and $\theta = \left(1+2n\right)$, and $$ \ln \left(-1\right) = \pi i\left(1+2n\right). $$

Solution 4:

$\pi$ is 180 degrees.

-1 is 180 degrees away from 1, around the complex plane's origin.

$e^{0i}$ is 1.

$e^{\theta i}$ is a point on the unity circle around the complex plane origin determined by the angle $\theta$, in radians. So if $\theta =\pi$, we get -1.

Complex exponentiation with other bases is also a rotation around the unity circle. For instance $5^{\phi i}$ also traces out a circle as we vary $\phi$. However, for such other bases, $\phi$, though an angle, isn't an angle measured in radians, and so $5^{\pi i}$ is not -1.

The correspondence between radians and the coefficient is only in the case of $e$.

$e$ is a special number which is inherently connected to the special number $\pi$ in multiple ways.

Solution 5:

Here are two ways of seeing this.

Consider the function $f(\theta)=e^{i \theta}$. Then $f''(\theta)=-f(\theta)$. Differential equations tell us that any such solution is a linear combination of $\sin(\theta)$ and $\cos(\theta)$ [reason:The Wronskiansk tells us that $f, \sin(x), \cos(x)$ are linearly dependent, while $\sin(x), \cos(x)$ are linearly independent].

Thus $f(\theta)=A \cos(\theta)+ B \sin(\theta)$ for some $A,B$. Setting $\theta=0$ Yields $A=1$, and derivating and setting $\theta=0$ Yields $B=i$.

Second apprroach

Let $f(x,y)=e^x (\cos(y)+i\sin(y))$.

Then $f(z_1+z_2)=f(z_1)f(z_2)$, and $f$ is continuous.Thus, $f$ is an exponential function. Since $f(1)=e$ we get that $f(z)=e^z$.

Note $f(z)$ satisfies the condition of CR- equations, and is $C_1$, thus it is analityc. Hence, it is the only analityc extension of $e^x$ to the complex plane.