What exactly does it mean for a function to be "well-behaved"?
In the sciences (as opposed to in mathematics) people are often a bit vague about exactly what assumptions they are making about how "well-behaved" things are. The reason for this is that ultimately these theories are made to be put to the test, so why bother worrying about exactly which properties you're assuming when what you care about is functions coming up in real life which are probably going to satisfy all of your assumptions.
This is particularly ubiquitous in physics where it is extremely common to make heuristic assumptions about well-behavior.
Even in mathematics we do this sometimes. When people say something is true for n sufficiently large, they often won't bother writing down exactly how large is sufficiently large as long as it's clear from context how to work it out. Similarly, in an economics paper you could read through the argument and figure out exactly what assumptions they need, but it makes it easier to read to just say "well-behaved."
The short answer is that there is no "exact" meaning. Ideally, additional axioms are introduced to ensure that a certain function (or any mathematical object, for that matter) is "well-behaved" which, in effect, makes analysis easier. So, the meaning of "well-behaved" should be derived from those specific additional axioms.
In general, we think of well-behaved functions as simpler, somehow. In any field, we might want to limit ourselves to considering only well-behaved functions in order to avoid having to deal with nasty edge cases. And in each of these domains, the community is free to choose whatever definition of 'well-behaved' makes sense for them. A quick look at the wiki link that e.James posted will show you the diversity in ideas of what it means to be well-behaved. I am no economist, so I will take for granted that the definition you put forth in your question is the one in common use.
I can see twice-differentiable as a reasonable requirement for a utility function to be 'well-behaved' is because the derivative of the utility function is marginal utility, and economists often care about the derivative of marginal utility. For example, if the second derivative of utility is negative, this means that the marginal utility has a negative derivative in other words, additional quantity of the good or service does not add utility as quickly. Also commonly referred to as diminishing returns.
If we want to be able to take the derivative even once, of course, we need the function to be continuous. You probably don't need to worry about the formal definition here. Pencil test should work fine.
The requirement for utility to be monotonic means that it is either always increasing or always decreasing. In other words, that a particular good or service is either desirable or not. If 10 widgets were good, 20 must be better. Of course, as mentioned above, maybe not that much better.
Monotonic means that it will also be quasi-concave. (Except for weird stuff like a flat function) That is, they have at most one local maximum. We would prefer that functions be quasiconcave because we wish to avoid cases like the one below. It just makes it so much easier to optimize when you only have one possible maximum to worry about.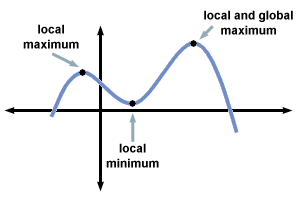
Globally non-satiated someone else can talk about. I don't know enough to be sure I won't just be misleading you further.
In practical application of mathematical analysis, the most useful "well-behavedness" condition on a function would be Lipshitz continuity. This ensures that the variations of a function are not too wild. The most important consequence is that differential equations will have a unique solution. All sorts of modelling of natural and physical situations uses differential equations, and it is valuable to know abstractly that they would have solutions under some tame conditions. Given such a theorem, one can concentrate exclusively on finding the solutions.