Rhetoric vs. Mathematics: ellipsis/ellipse, parable/parabola, hyperbole/hyperbola

Do ellipsis, parable, and hyperbole from rhetoric have anything in common with the geometric curves ellipse, parabola, and hyperbola used in mathematics?

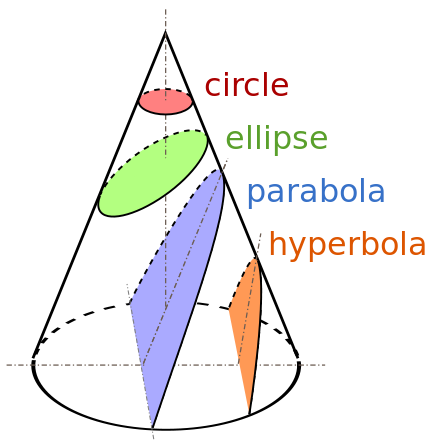
There are three geometric curves known as conic sections:

1. Ellipse: a curve on a plane surrounding two focal points such that a straight line drawn from one of the focal points to any point on the curve and then back to the other focal point has the same length for every point on the curve.

2. Parabola: a two-dimensional, mirror-symmetrical curve, which is approximately U-shaped when oriented as shown in the diagram.

3. Hyperbola: has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows.

There are also three terms in linguistics with analogous names (in many languages with the same names, actually):

1. Ellipsis: the omission from a clause of one or more words that are nevertheless understood in the context of the remaining elements.

   • John can play the guitar, and Mary can play the violin.

2. Parable: a succinct, didactic story, in prose or verse, which illustrates one or more instructive lessons or principles.

   • The Emperor's New Clothes

3. Hyperbole: is the use of exaggeration as a rhetorical device or figure of speech.

   • That suitcase weighed a ton!

Do they have anything in common? Is there any etymological or other reason connecting each pair together? Does the ellipsis remind the ellipse in any way, etc.? Is there any analogy between them?

Solution 1:

In Ancient Greek, where both the rhetorical and geometrical terms were invented, they are the same words, employed in different figurative senses:

• A ‘parabole’ is a ‘casting/setting side by side’—using Latin-derived morphs an ‘apposition’ or ‘adjacency’. In rhetoric, it is a comparison, which sets two terms side-by-side; later it denotes a fiction which is ‘set beside’ and parallels (‘lies next to’) reality. In geometry, it is a conic section formed by the intersection of a cone with a plane with the same inclination to the axis as one of the cone’s sides—the plane is parallel to that side.
• A ‘hyperbole’ is a literally a ‘casting/setting above’, more generally an excess. In rhetoric it is an exaggeration, something which speaks of something in excessive terms. In geometry it is another conic section formed by the intersection of a plane with both branches of a cone, in which the inclination of the cutting plane to the axis exceeds that of the cone’s side
• An ‘ellipsis’ is a ‘falling short, deficiency’. In rhetoric, it denotes the omission of one or more words needed to complete the sense—the utterance thus falls short of completion. In geometry it is a conic section in which the cutting plane’s inclination is less than—falls short of—the inclination of the cone’s side.

Solution 2:

These English terms derive indirectly from the respective Ancient Greek origins:

• ἔλλειψις (elleipsis): falling short / omission
• παρά- (pará-): "alongside" or "application"
• ὐπερ- (huper-): "exceed"

The relationship of the rhetorical terms with these origins should be self-evident. I'll focus on the conic sections instead.

We know that the conic sections were referred to by cognates of their current English names by Apollonius of Perga (c. 200 BCE). It is unclear whether he coined those terms, or whether they were already in use at the time. The exact reason why those words were chosen is also a matter of educated speculation; Jeff Miller cites some sources.

One straightforward explanation is that the terms for the conic sections refer to the angle between the cone and the cutting plane. If the cutting plane is parallel to exactly one generating line of the cone, then the conic is unbounded and is called a parabola. If the plane intersects at a smaller angle, it is an ellipse; if it intersects at a larger angle, it is a hyperbola.

However, the explanation for parabola might be more complicated. According to Online Etymology Dictionary,

parabola (n.)

1570s, from Modern Latin parabola, from Greek parabole "parabola, comparison, analogy; application" (see parable), so called by Apollonius of Perga c.210 B.C.E. because it is produced by "application" of a given area to a given straight line. It had a different sense in Pythagorean geometry. Related: Parabolic.

That explanation is a bit of an enigma, requiring an illustration from Wikipedia to understand. The blue rectangle has the same area as the orange square, and the rectangle's projected width on the x-axis stays a constant width.

Conic sections can also be classified by their eccentricity:

• The eccentricity of an ellipse [is] less than 1.
• The eccentricity of a parabola is 1.
• The eccentricity of a hyperbola is greater than 1.

Although the eccentricity explanation is also simple and appealing, it is uncertain whether that is what Apollonius (or whoever) had in mind when coining the terms for the conic sections.