Which mathematicians have influenced you the most? [closed]

This question is lifted from Mathoverflow.. I feel it belongs here too.

There are mathematicians whose creativity, insight and taste have the power of driving anyone into a world of beautiful ideas, which can inspire the desire, even the need for doing mathematics, or can make one to confront some kind of problems, dedicate his life to a branch of math, or choose an specific research topic.

I think that this kind of force must not be underestimated; on the contrary, we have the duty to take advantage of it in order to improve the mathematical education of those who may come after us, using the work of those gifted mathematicians (and even their own words) to inspire them as they inspired ourselves.

So, I'm interested on knowing who (the mathematician), when (in which moment of your career), where (which specific work) and why this person had an impact on your way of looking at math. Like this, we will have an statistic about which mathematicians are more akin to appeal to our students at any moment of their development. Please, keep one mathematician for post, so that votes are really representative.

Leonhard Euler

• He made important discoveries in pretty much every mathematical field there was at his time.

• He discovered graph theory.

• He is responsible for much of the current mathematical notation we use today, including Σ, i, e, f(x), π, and sin/cos.

• EVERYTHING is named after him

• His combined works fill 80 (!) volumes.

• And last but not least,

  

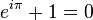
Srinivasa Ramanujan

These quotes says it all

Quoting K. Srinivasa Rao, "As for his place in the world of Mathematics, we quote Bruce C. Berndt: 'Paul Erdős has passed on to us Hardy's personal ratings of mathematicians. Suppose that we rate mathematicians on the basis of pure talent on a scale from 0 to 100, Hardy gave himself a score of 25, J.E. Littlewood 30, David Hilbert 80 and Ramanujan 100.'"

"In mathematics, there is a distinction between having an insight and having a proof. Ramanujan's talent suggested a plethora of formulae that could then be investigated in depth later. It is said that Ramanujan's discoveries are unusually rich and that there is often more to them than initially meets the eye."

Hardy said : "The limitations of his knowledge were as startling as its profundity. Here was a man who could work out modular equations and theorems... to orders unheard of, whose mastery of continued fractions was... beyond that of any mathematician in the world, who had found for himself the functional equation of the zeta function and the dominant terms of many of the most famous problems in the analytic theory of numbers; and yet he had never heard of a doubly periodic function or of Cauchy's theorem, and had indeed but the vaguest idea of what a function of a complex variable was..."

Emmy Noether

I find it surprising, given Hilbert's mention, that nobody's yet included his most famous algebraist associate.

Over the course of a busy and prolific mathematical career, Noether revolutionised abstract algebra. (It is impossible to describe the limits of her influence on modern abstract algebra; there are none.) She performed nearly as brilliantly in topology. Noether's Theorem is critical in the development of modern physics of dynamical systems.

But I find her inspiring for her skill as a teacher. Noether was a determined and passionate teacher, who led lectures by discussing current active problems openly and in detail with her students. She was also known for being endlessly patient with her students, and several of her students went on to make critical contributions of their own. (When the Nazis made it impossible for a Jew to teach at university, she calmly shifted to holding classes at her house - and then moved to Princeton, returning to Gottingen only as a visiting foreign academic.)

Noether was profilic and generous with her ideas, frequently passing critical work, and credit for her ideas, to students or colleagues - even when it meant developing their careers ahead of her own. This means she had a direct and indirect impact in several fields superficially unrelated to the work she's most famous for. (All this despite dealing with the misogynist prejudices of her time, which lead to her working unpaid at Gottingen for years, and lecturing under Hilbert's name rather than her own.)