How to find measurements of angle CBD?

I got $x + CBD = 110^{o}$. I think I should find measurements of angle CBD, so how to find it? Do you have any ideas? Please help me!

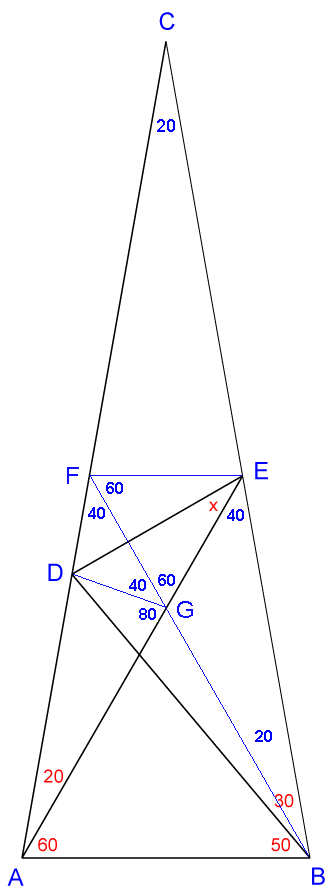
1. $\angle ACB = 180^\circ-(10^\circ+70^\circ)-(60^\circ+20^\circ) = 20^\circ$ and $\angle AEB = 180^\circ-60^\circ-(50^\circ+30^\circ) = 40^\circ$.
2. Draw a line from point $E$ parallel to $AB$, labeling the intersection with $AC$ as a new point $F$ and conclude $\Delta CEF\sim\Delta ABC$, \begin{align} \angle CEF &= \angle CBA = 50^\circ+30^\circ = 80^\circ\\ \angle FEB &= 180^\circ-80^\circ = 100^\circ\\ \angle AEF &= 100^\circ-40^\circ = 60^\circ\\ \angle CFE &= CAB = 60^\circ+20^\circ = 80^\circ\\ \angle EFA &= 180^\circ-80^\circ = 100^\circ \end{align}
3. Draw a line $FB$ labeling the intersection with $AE$ as a new point $G$ and conclude $\Delta AFE\cong\Delta BEF$, \begin{align} \angle AFB &=\angle BEA = 40^\circ\\ \angle BFE &= \angle AEF = 60^\circ\\ \angle FGE &= 180^\circ-60^\circ-60^\circ = 60^\circ = \angle AGB\\ \angle ABG &= 180^\circ-60^\circ-60^\circ = 60^\circ\\ \end{align}
4. Draw a line $DG$. Since $AD=AB$ (leg of isosceles) and $AG=AB$ (leg of equilateral), conclude $AD = AG$, $\Delta DAG$ is isosceles and $$ \angle ADG =\angle AGD = \frac{180^\circ-20^\circ}2 = 80^\circ. $$
5. Since $\angle DGF = 180^\circ-80^\circ-60^\circ = 40^\circ$, conclude $\Delta FDG$ (with two $40^\circ$ angles) is isosceles, so $DF = DG$.
6. With $EF = EG$ (legs of equilateral) and $DE = DE$ (same line segment) conclude $\Delta DEF\cong\Delta DEG$ by side-side-side rule, $\angle DEF =\angle DEG = x$, and $$ \angle FEG = 60^\circ = x+x\quad\Rightarrow\quad \large\color{blue}{x=30^\circ}. $$