The 'sine and cosine theorem' - formulas for the sum and difference

I've read somewhere that the sine and cosine functions can be fully described by this theorem:

1. $\sin(0) = 0, \cos(0) = 1$
2. $\sin(a-b) = \sin(a)\cos(b) - \sin(b)\cos(a)$
3. $\cos(a-b) = \cos(a)\cos(b) + \sin(a)\sin(b)$
4. There is na $r>0$ such that: $$0<\sin(x)<x<\tan(x), x \in(0, r), \tan(x) = \frac{\sin(x)}{\cos(x)} $$

With this theorem, we can prove things like:

• $\sin^2(x) + \cos^2(x) = 1$ by doing $\cos(a-a) = \cos(a)\cos(a) + \sin(a)\sin(a)$

• $\sin(-x) = -\sin(x)$ by doing $\sin(0-x) = \sin(0)\cos(x) - \sin(x)\cos(0)$

• $\cos(a+b) = \cos(a)\cos(b) - \sin(a)\sin(b)$

  by doing

  $\cos(a-(-b)) = \cos(a)\cos(-b) + \sin(a)\sin(-b)$

• $\sin(a+b) = \sin(a)\cos(b)+\sin(b)\cos(a)$

  by doing

  $\sin(a-(-b)) = \sin(a)\cos(-b) - \sin(-b)\cos(a)$

And other trigonometric identities that also follows from what I've already done.

The problem is that there are many definitions for the sine and cosine function. Let's begin by the classical definition:

Classical Definition

The sine function is defined as the ratio between the opposite side of the angle, and the hipotenuse of this right triangle.

The cosine function is defined as the ratio between the adjacent side of the angle, and the hipotenuse of this right triangle.

The tangent function is defined as the ratio between the sine function and the cosine function (with $\cos (x) \neq 0)$

The other trigonometric identities can be proven geometrically for an angle less than or equal $\frac{\pi}{2}rad$ because it's a right triangle. So, we can't prove $\sin(a-b)$ geometrically and then prove $\sin(a+b)$ analytically like I did, because we assumed a negative $b$, something that's not defined geometrically in the right triangle.

The identity $\sin^2(x) + \cos^2(x) = 1$ can be proven with a simple pythagorean theorem in a triangle with hypotenuse 1.

The formulas for the sum and difference of sines and cosines can be proven geometrically like in this images I found in this answer:

Unit circle definition

Imagine a circle centered at the origin of the cartesian plane, then:

The sine function for an $x \in R, x>0$ can be defined as the $y$ position of point of the circle where the angle stops if we travel anti-clockwise inside the circle's line.

The cosine for an $x \in R, x>0$ function can be defined as the $x$ position of point of the circle where the angle stops if we travel anti-clockwise inside the circle's line.

We can make the same definition for negative angles, so for an $x \in R, x<0$ the same holds, but we're know travelling clockwise.

The tangent function is defined as the ratio between the sine function and the cosine function (with $\cos (x) \neq 0)$

Then, we can define these functions for all real numbers, since when we travel $2\pi$ we get back to the initial point. So we defined sine and cosine as periodic functions.

Open question: How do I prove, with the unit circle periodic definition and without being circular, the $\sin(a-b)$ and $\cos(a-b)$ formulas? (same for $\sin(a+b)$ and $\cos(a+b)$.

Taylor Series definition

$$\sin x = \sum^{\infty}_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1}$$ $$\cos x = \sum^{\infty}_{n=0} \frac{(-1)^n}{(2n)!} x^{2n}$$ $$\tan x = \sum^{\infty}_{n=1} \frac{B_{2n} (-4)^n (1-4^n)}{(2n)!} x^{2n-1}$$

Here, in the same question, there's an analytic proof of the trigonometric identites, for these sums.

What's the best definition for calculus?

Well, in calculus we use trigonometric functions a LOT: in integral substitutions, in series, taylor series (like the ones I showed now), derivatives, convergence tests (like the Euler onde in the basel problem) and other things...

All the definitions I see, are kinda circular or not rigorous enough to make me feel good taking some derivatives or integral substitution, because I always care about the domain of these things. So I want to define it very nicely and be able to use all the trigonometric identities.

I've seen many geometrical proofs of $\sin(a-b)$, $\sin(a+b)$, $\cos(a-b)$, $\cos(a+b)$ using a right triangle and then suddenly the person starts using this formula for all real numbers. I need a complete definition of the trigonometric functions that works periodically and for all reals. The taylor series definition seems good but they're generated using trigonometric identities that are not yet proven (assuming this definition).

ps: I know that I used some primitive words in some definitions, like 'travel' so I let them in emphasis, but I hope you guys understand. And sorry by the long post, but I needed to do it, because I've never seen a complete definition in any book. Thanks.

The standard definition of the trig functions is in terms of a unit circle. The classical definition in terms of right triangles is more limited in terms of scope. For this reason in Calculus the more robust definition in terms of the unit circle is used. From this 'standard' definition every identity about the trigonometric functions can be proven.

In your post above you gave the definition in terms of the unit circle, but you left what I think is an important point. When defined in terms of the unit circle the trig functions are 'real valued'. What we mean here is that they are defined in terms of a distance and not some constructed idea called an angle. So let me begin with the definition in terms of the unit circle, then we will move to the sister proof to the one given above for the sine of a difference. From this we can establish the other three identities.

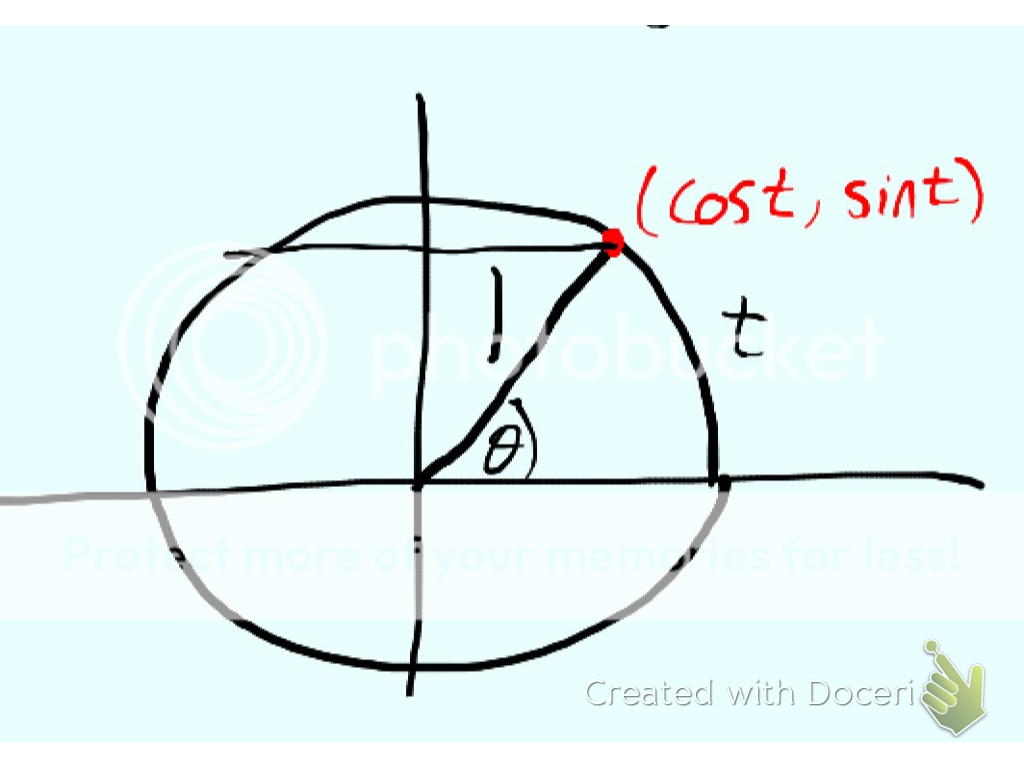
Consider the unit circle $$ \begin{equation}x^2+y^2 = 1 \end{equation} $$ Starting at the x-intercept (1,0) we travel a distance t around the circle in a counter-clockwise direction (a clockwise movement would be assigned a negative sign). Once we travel a distance t around the circle we end at a point P(x,y) on the circle. We then define $$ \begin{eqnarray} \cos t = x \\ \sin t = y \end{eqnarray} $$

It then turns out that we can return to angles by noting that on the unit circle the radian measure of the central angle subtended by the arc of length t is equal to t. But we don't need to ever actually return to angles. Our definition stands on its own. Now an immediate consequence of our definition is the familiar Pythagorean identity for sine and cosine.
$$\begin{equation} \cos^2 t + \sin^2 t = 1 \end{equation} $$
(This is obtained by substituting sine and cosine into the unit circle equation for x and y.)

Before we move onto the identity you asked about first let us notice that the sine and cosine functions are periodic. IE. $$ \cos(a + 2k \pi) = \cos a $$. I believe this is pretty clear because any trip around the circle will take you back to where you started. Make that trip k times and you are still back where you started. For this reason as mentioned above we can assume both angles are in$$ [0, 2 \pi)$$. Also note that $$\cos (-t) = \cos t $$ for all real numbers t.

The last thing to address is that rotation is a rigid transformation. In other words when we rotate the plane about a point, the distance between two points before rotation is the same after rotation.

Now we return to the problem. Show that
$$\cos(a-b) = \cos a \cos b + \sin a \sin b $$
Without loss of generality assume $$0<b<a<2 \pi $$ (the case of b=0 is trivial, as is the case of a = 2 $\pi$, and the case a=b, you can verify these yourself)

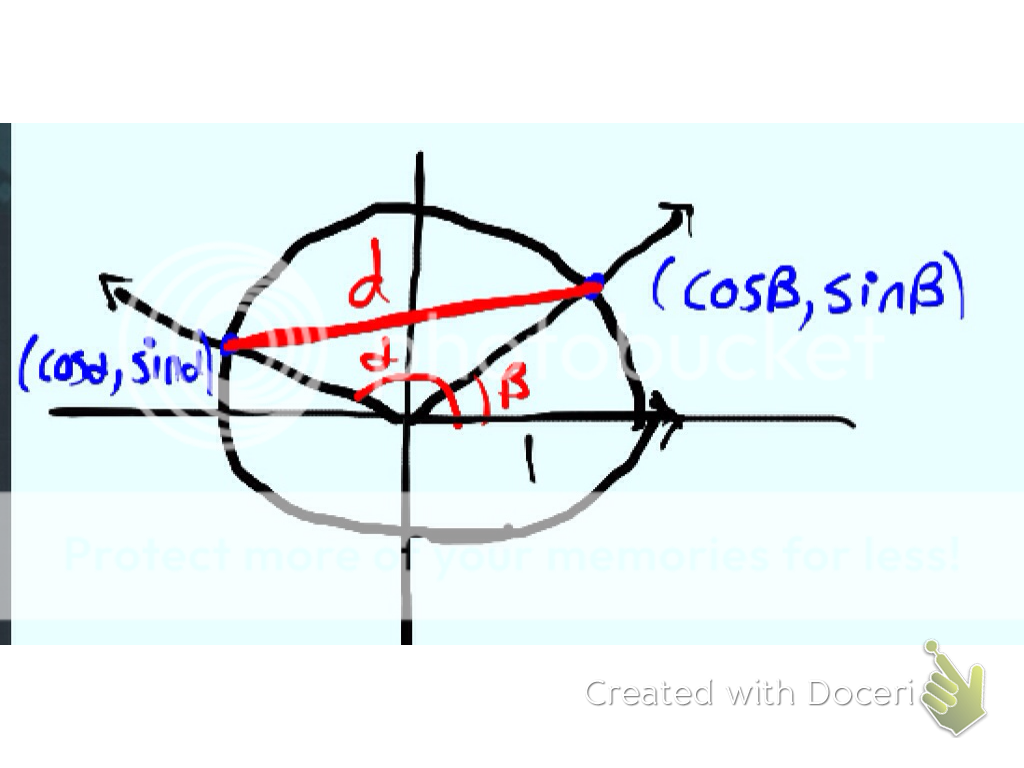
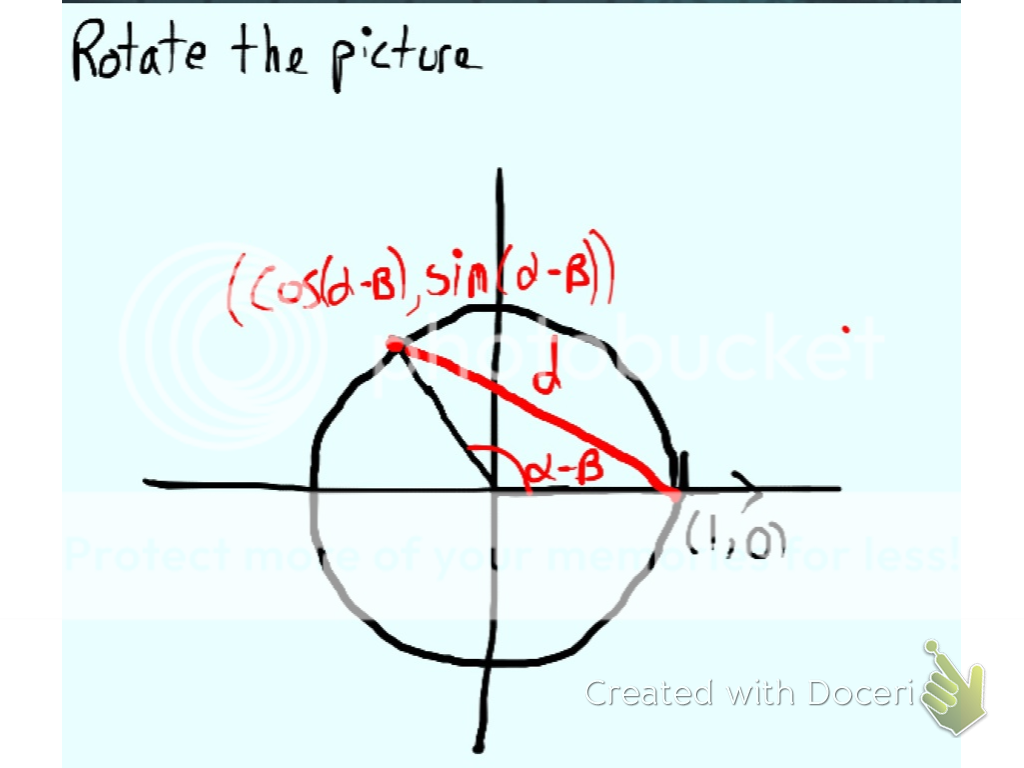
We now consider the points (see diagrams) P($\cos a, \sin b)$ and Q($\cos b, \sin b)$ on the unit circle. We can use the distance formula to find the length of segment PQ. We then rotate the entire plane clockwise through a distance b along the circumference of the circle (or through an angle with radian measure b). This will place point Q at Q`(1,0) and P will now be a distance b-a along the circle from (1,0) so it will be at P`($\cos(a-b), \sin(a-b))$. We now proceed to use the distance formula. Since distance is preserved through rotation segment PQ and segment P`Q` will have the same length.

$$\begin{eqnarray} \sqrt{(\cos a - \cos b)^2 + (\sin a - \sin b)^2} = \sqrt{(\cos(a-b)-1)^2 + (\sin(a-b) - 0)^2} \\ \cos^2 a - 2 \cos a \cos b + \cos^2 b + \sin^2 a - 2 \sin a \sin b + \sin^2 b = \cos^2(a-b) - 2 \cos(a-b) + 1 + \sin^2(a-b) \\ \cos^2 a + \sin^2 a + \cos^2 b + \sin^2 b - 2 \cos a \cos b - 2 \sin a \sin b = \cos^2(a-b) + \sin^2(a-b) + 1 - 2 \cos(a-b) \\ - 2 \cos a \cos b - 2 \sin a \sin b = - 2 \cos(a-b) \\ \cos a \cos b \sin a \sin b = \cos(a-b) \end{eqnarray} $$

Now I assumed $b<a$, is that ok? The answer is yes but you might want to answer why.

Armed with the cosine of the difference formula we can now prove the following.

$$ \begin{eqnarray} \cos(a+b) = \cos(a-(-b)) = \cos a \cos(-b) - \sin a \sin(-b) \\ = \cos a \cos b - \sin a \sin b \end{eqnarray} $$

The last step in the equality comes from our identity for $\cos(-t)$ above and the fact that $\sin(-t) = -\sin(t) $ as was mentioned in the previous post.

Now we can show that $\cos(\frac{\pi}{2} - x) = \sin x$ and in a similar manner to the problem above that $\sin(\frac{\pi}{2} - x) = cos x$. These are your familiar co-function identities. Finally armed with these equations we can now demonstrate the sine of a difference which can then prove the sine of a sum formula.

$$ \begin{eqnarray} \sin(a-b) = \cos(\frac{\pi}{2} - (a-b)) \\ = \cos((\frac{\pi}{2} -a) + b) \\ = \cos(\frac{\pi}{2} -a) \cos b - \sin(\frac{\pi}{2} -a) \sin b \\ = \sin a \cos b - \cos a \sin b \end{eqnarray} $$

And so there we have it. I apologize if the formating is off a bit, still getting used to the system. But now from this identities you can prove most any other basic identity involving the trig functions. All of your double and half angle formulas and your sum-product and product-sum formulas.

I. I think that, at the point you're at, you'll be most satisfied at first with a development of the theory of trigonometric functions that starts with geometric considerations and builds up from there. For this I know two approaches:

First, you can start with ratios of sides in right triangles, defining the functions first for acute angles and then extending them carefully to larger domains. The only place I've seen this done in detail is the little book Trigonometry, by Gelfand and Saul, which I highly recommend (even though it's a textbook for children). One very nice feature is that they give the right reasons for choosing the extensions they do — e.g., they justify the extension of sine from $[0^\circ,90^\circ]$ to $[0^\circ,180^\circ]$ by noting that it's the only way for the law of sines to be correct also for obtuse triangles. The addition law is Ptolemy's theorem, for some range of angles, and then the extensions are chosen to make it valid everywhere.

Alternatively, you can derive an integral formula for the area of a circular sector, then use that function to define sine and cosine. This is done carefully in chapter 15 of Spivak's Calculus.

II. Now, once you've got everything on a firm foundation like that, you can renovate: choose some proved property of sine and/or cosine which completely determine those functions, take it as a new definition of those functions, and rebuild the theory on that basis. Of course, this only makes sense when you already know that the functions you're interested in have those properties (because you proved it from the old definition), since otherwise you're left wondering how we know that these newly defined functions are the same ones as the ones we already knew — but internally it holds up by its own logic. Sometimes this kind of renovation can make the theory more elegant, sometimes it allows the use of the functions in a new context where the old definition is nonsensical, sometimes it's just neat. Here are a few such properties:

First, sine is the only function $f$ satisfying

• $f''=-f$
• $f(0)=0$
• $f'(0)=1$

(See Spivak's Theorem 4. He proves the addition law not from his definition, but from these properties, quite tidily indeed. You could view his definition as merely a technical matter of showing that some function having these properties exists, which could also be handled by the theory of differential equations.)

Second, you can define sine and cosine by their power series. This is a very good approach if you're going to use them with complex numbers.

Third, $$ \sin x = \frac{e^{ix} - e^{-ix}}{2i} $$ so if you've defined the complex exponential somehow, you can get the trig functions. (Of course defining the complex exponential involves much the same types of considerations.)

Fourth, given a positive real number $p$, there is exactly one pair of functions $S,C$ satisfying

• $C(x-y)=C(x)C(y)+S(x)S(y)$
• $S(p)=1$
• $S(x)\ge 0$ for all $x\in [0,p]$.

This is the main result of G. B. Robison, "A New Approach to Circular Functions, $\pi$ and $\lim (\sin x)/x$", Math. Mag. 41 (1968), 66–70 (jstor). Taking $p=\frac\pi2$ yields the usual sine and cosine functions. (Actually the author suggests first taking $S$ and $C$ to be the functions obtained with $p=1$, and then defining $\pi = 2\lim_{x\to 0} S(x)/x$.) The paper proves all the usual basic trigonometric identities along the way — except, of course, for the identity for $\cos(x-y)$, since that's the definition!

Robison refers to a slightly earlier paper (W. F. Eberlein, "The Circular Function(s)", Math. Mag. 39 (1966), 197–201) which essentially defines arctan first (by an integral, as suggested in comments), then uses it to define the function which would usually be written $x\mapsto e^{ix}$, and thence sine and cosine.

III. You asked specifically how to prove the addition formulas from the unit circle definition. My favourite (but not quite fully rigorous) method is this: the unit circle definition amounts to saying that if $R_\theta$ denotes counterclockwise rotation about the origin by $\theta$ radians then $$ R_\theta\left[\begin{matrix} 1 \\ 0 \end{matrix}\right] = \left[\begin{matrix} \cos\theta \\ \sin\theta \end{matrix}\right] $$ With a little geometry you can show also that $$ R_\theta\left[\begin{matrix} 0 \\ 1 \end{matrix}\right] = \left[\begin{matrix} -\sin\theta \\ \phantom-\cos\theta \end{matrix}\right] $$ You can prove that $R_\theta$ is linear (say, because it's an isometry that fixes the origin). So it has a matrix, and the above two statements show that this matrix is $$ \left[\begin{matrix} \cos\theta & -\sin\theta \\ \sin\theta & \phantom-\cos\theta \end{matrix}\right] $$ Now, it's intuitively obvious that $R_{a+b}=R_a\circ R_b$; therefore $$ \left[\begin{matrix} \cos (a+b) & -\sin (a+b) \\ \sin (a+b) & \phantom-\cos (a+b) \end{matrix}\right] = \left[\begin{matrix} \cos a & -\sin a \\ \sin a & \phantom-\cos a \end{matrix}\right] \left[\begin{matrix} \cos b & -\sin b \\ \sin b & \phantom-\cos b \end{matrix}\right] $$ Multiplying the matrices on the RHS and identifying corresponding entries gives you the addition formulas. [Edit: And, of course, this is in the linked question.]

The most straightforward definition is from $e^z$.

First define $e^z = \sum_{k=0}^\infty \frac{z^n}{n!}$, and prove that $e^{z+z'}=e^ze^{z'}$ using a Cauchy product. You also get at once that the derivative of $e^z$ is $e^z$.

Define $\cos z = \frac{e^{iz}+e^{-iz}}{2}$, $\sin z = \frac{e^{iz}-e^{-iz}}{2i}$, and similarly $\cosh z = \frac{e^{z}+e^{-z}}{2}$, $\sinh z = \frac{e^{z}-e^{-z}}{2}$. You will have trivially the derivatives of these functions. As a side remark, this eliminates the usual problem with $\lim_{x\rightarrow 0} \frac{\sin x}{x}=1$, when defining trig functions geometrically.

From the formula $e^{z+z'}=e^ze^{z'}$, you can derive most usual trigonometric formulas (except those involving $\pi$, which is yet to be defined). You will get almost the same formulas for hyperbolic trigonometry.

Notice $\cos z$ and $\sin z$ are real valued for real $z$. From series definition you know they are $C^\infty$ on $\Bbb R$, and especially, they are continuous. You have $\cos 0 = 1$ and it's easy to prove that $\cos 2<0$, thus $\cos$ has a root in $]0, 2[$. Similarly you can prove that $\sin x > 0$ in this interval, and from $\cos'=-\sin$, you know $\cos$ has only one root. Call it $\frac{\pi}{2}$ (that is, define $\pi$ to be twice the root). Then from addition formulas, it's easy to prove $\cos$ and $\sin$ are $2\pi$-periodic.

Then you are done with the main properties of these functions. If you like, you can also define $\tan x$ and all other lesser known function (secant, cosecant, cotangent), and derive formulas for $\tan (x+y)$ and alike. And define inverse trig functions (well, strictly speaking, they are inverses of restrictions of trig functions to carefully chosen intervals, so that they are bijective on them), etc.

My recollection from high school math is that for calculus, we relied on the unit-circle definition, which agrees with the classical definition of sine and cosine for angles in the range $[0, \pi/2]$ as long as you accept that the measure of the angle is the same as the length of the intercepted arc.

On the unit circle, traveling a distance $2\pi$ brings you back to your starting point, so you can show that if $\sin \theta = y$, then $\sin (\theta + 2n\pi) = y$ for any integer $n$. You can then show by means of congruent triangles (reflected across the $x$-axis) that $\sin(-x) = -\sin x$ for any real number $x$.

So without loss of generality, in evaluating $\sin(a - b)$ we can assume that $-\pi < a - b \le \pi$. We can easily solve the cases $a - b = 0$ and $a - b = \pi$. Moreover, whenever $-\pi < a - b < 0$, we can use the fact that $\sin(a - b) = -\sin(b - a)$, so really we only need to find the formula for $\sin(a - b)$ in the case where $0 < a - b < \pi$.

Let $O$ be the center of the circle, let $A$ be the point you reach after traveling the distance $a$ counterclockwise on the circle, and let $B$ be the point reached after traveling distance $b$. Then $\triangle AOB$ is a triangle whose angle at $O$ is $a - b$. We now apply the following transformation to the $x$ and $y$ coordinates of $A$ and $B$:

\begin{eqnarray} x \rightarrow x \cos b + y \sin b, \\ y \rightarrow y \cos b - x \sin b. \end{eqnarray}

Let $A'$ and $B'$ be the points whose coordinates are produced by applying this transformation to the coordinates of $A$ and $B$, respectively. Since the coordinates of $B$ are $(\cos b, \sin b)$, we can show that the coordinates of $B'$ are $(1, 0)$. We can use the Pythagorean formula on pairs of coordinates to prove that the distance from $O = (0,0)$ to $A'$ is $1$, and that the distance from $A'$ to $B'$ equals the distance from $A$ to $B$, and now we know that the triangles $\triangle AOB$ and $\triangle A'OB'$ are congruent. Therefore the angle at $O$ in $\triangle A'OB'$ has measure $a - b$. Meanwhile, we can find that the $y$-coordinate of $A'$ is $\sin a \cos b - \cos a \sin b$. It just remains to show that $\triangle AOB$ and $\triangle A'OB'$ have the same orientation (so that $A'$ is above the $x$-axis), which you can do by applying a formula on the coordinates of the vertices of a triangle that gives the triangle's orientation (that is, the outcome is multiplied by $-1$ if you reflect the triangle), or by other knowledge of isometries. Once we know this, we have shown that

\begin{equation} \sin(a - b) = \sin a \cos b - \cos a \sin b. \end{equation}

A similar procedure works for the cosine difference formula, though in this case we don't have to show that $A'$ is above the axis:

\begin{equation} \cos(a - b) = \cos a \cos b - \sin a \sin b. \end{equation}

For $\sin(a + b)$ and $\cos(a + b)$, just substitute $-b$ for $b$ in the formulas already known.