High quality, simple random password generator

The difficult thing with passwords is to make them strong enough and still be able to remember them. If the password is not meant to be remembered by a human being, then it is not really a password.

You use Python's os.urandom(): that's good. For any practical purpose (even cryptography), the output of os.urandom() is indistinguishable from true alea. Then you use it as seed in random, which is less good: that one is a non-cryptographic PRNG, and its output may exhibit some structure which will not register in a statistical measurement tool, but might be exploited by an intelligent attacker. You should work with os.urandom() all along. To make things simple: choose an alphabet of length 64, e.g. letters (uppercase and lowercase), digits, and two extra punctuation characters (such as '+' and '/'). Then, for each password character, get one byte from os.urandom(), reduce the value modulo 64 (this is unbiased because 64 divides 256) and use the result as index in your chars array.

With an alphabet of length 64, you get 6 bits of entropy per character (because 2⁶ = 64). Thus, with 13 characters, you get 78 bits of entropy. This is not ultimately strong in all cases, but already very strong (it could be defeated with a budget which will be counted in months and billions of dollars, not mere millions).

XKCD has a great explanation of why what you think are strong passwords aren't.

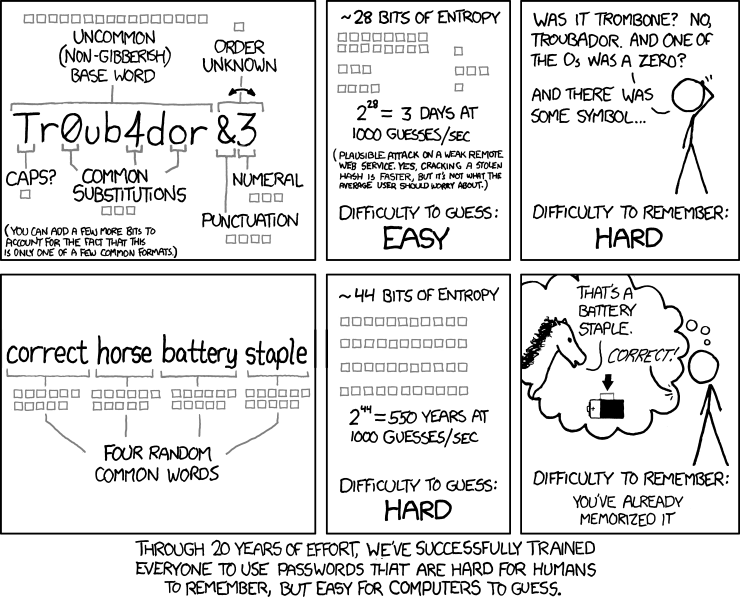
To anyone who understands information theory and security and is in an infuriating argument with someone who does not (possibly involving mixed case), I sincerely apologize. - Randall Munroe

And if you don't understand the math behind what this illustration is explaining, don't try writing anything that should be cryptographically secure, because it won't be. Just put the mouse down and step away from the keyboard.

FYI for anyone running across this question in the year 2020+. Python 3.6+ has a secrets module specifically for this purpose:

import secrets

password_length = 13
print(secrets.token_urlsafe(password_length))

Just two days ago, Kragen Javier Sitaker posted a program to do this at http://lists.canonical.org/pipermail/kragen-hacks/2011-September/000527.html (gone now - try https://github.com/jesterpm/bin/blob/master/mkpasswd)

Generate a random, memorizable password: http://xkcd.com/936/

Example run:

kragen at inexorable:~/devel/inexorable-misc$ ./mkpass.py 5 12 Your password is "learned damage saved residential stages". That's equivalent to a 60-bit key.

That password would take 2.5e+03 CPU-years to crack on my inexpensive Celeron E1200 from 2008, assuming an offline attack on a MS-Cache hash, which is the worst password hashing algorithm in common use, slightly worse than even simple MD5.

The most common password-hashing algorithm these days is FreeBSD’s iterated MD5; cracking such a hash would take 5.2e+06 CPU-years.

But a modern GPU can crack about 250 times as fast, so that same iterated MD5 would fall in 2e+04 GPU-years.

That GPU costs about US$1.45 per day to run in 2011, so cracking the password would cost about US$3e+09.

I've started using a password generated this way in place of a 9-printable- ASCII-character random password, which is equally strong. Munroe's assertion that these passwords are much easier to memorize is correct. However, there is still a problem: because there are many fewer bits of entropy per character (about 1.7 instead of 6.6) there is a lot of redundancy in the password, and so attacks such as the ssh timing-channel attack (the Song, Wagner, and Tian Herbivore attack, which I learned about from Bram Cohen in the Bagdad Café in the wee hours one morning, years ago) and keyboard audio recording attacks have a much better chance of capturing enough information to make the password attackable.

My countermeasure to the Herbivore attack, which works well with 9-character password but is extremely annoying with my new password, is to type the password with a half-second delay between characters, so that the timing channel does not carry much information about the actual characters used. Additionally, the lower length of the 9-character password inherently gives the Herbivore approach much less information to chew on.

Other possible countermeasures include using Emacs shell-mode, which prompts you locally for the password when it recognizes a password prompt and then sends the whole password at once, and copying and pasting the password from somewhere else.

As you'd expect, this password also takes a little while longer to type: about 6 seconds instead of about 3 seconds.

#!/usr/bin/python
# -*- coding: utf-8 -*-

import random, itertools, os, sys

def main(argv):
    try:
        nwords = int(argv[1])
    except IndexError:
        return usage(argv[0])

    try:
        nbits = int(argv[2])
    except IndexError:
        nbits = 11

    filename = os.path.join(os.environ['HOME'], 'devel', 'wordlist')
    wordlist = read_file(filename, nbits)
    if len(wordlist) != 2**nbits:
        sys.stderr.write("%r contains only %d words, not %d.\n" %
                         (filename, len(wordlist), 2**nbits))
        return 2

    display_password(generate_password(nwords, wordlist), nwords, nbits)
    return 0

def usage(argv0):
    p = sys.stderr.write
    p("Usage: %s nwords [nbits]\n" % argv0)
    p("Generates a password of nwords words, each with nbits bits\n")
    p("of entropy, choosing words from the first entries in\n")
    p("$HOME/devel/wordlist, which should be in the same format as\n")
    p("<http://canonical.org/~kragen/sw/wordlist>, which is a text file\n")
    p("with one word per line, preceded by its frequency, most frequent\n")
    p("words first.\n")
    p("\nRecommended:\n")
    p("    %s 5 12\n" % argv0)
    p("    %s 6\n" % argv0)
    return 1

def read_file(filename, nbits):
    return [line.split()[1] for line in
            itertools.islice(open(filename), 2**nbits)]

def generate_password(nwords, wordlist):
    choice = random.SystemRandom().choice
    return ' '.join(choice(wordlist) for ii in range(nwords))

def display_password(password, nwords, nbits):
    print 'Your password is "%s".' % password
    entropy = nwords * nbits
    print "That's equivalent to a %d-bit key." % entropy
    print

    # My Celeron E1200
    # (<http://ark.intel.com/products/34440/Intel-Celeron-Processor-E1200-(512K-Cache-1_60-GHz-800-MHz-FSB)>)
    # was released on January 20, 2008.  Running it in 32-bit mode,
    # john --test (<http://www.openwall.com/john/>) reports that it
    # can do 7303000 MD5 operations per second, but I’m pretty sure
    # that’s a single-core number (I don’t think John is
    # multithreaded) on a dual-core processor.
    t = years(entropy, 7303000 * 2)
    print "That password would take %.2g CPU-years to crack" % t
    print "on my inexpensive Celeron E1200 from 2008,"
    print "assuming an offline attack on a MS-Cache hash,"
    print "which is the worst password hashing algorithm in common use,"
    print "slightly worse than even simple MD5."
    print

    t = years(entropy, 3539 * 2)
    print "The most common password-hashing algorithm these days is FreeBSD’s"
    print "iterated MD5; cracking such a hash would take %.2g CPU-years." % t
    print

    # (As it happens, my own machines use Drepper’s SHA-2-based
    # hashing algorithm that was developed to replace the one
    # mentioned above; I am assuming that it’s at least as slow as the
    # MD5-crypt.)

    # <https://en.bitcoin.it/wiki/Mining_hardware_comparison> says a
    # Core 2 Duo U7600 can do 1.1 Mhash/s (of Bitcoin) at a 1.2GHz
    # clock with one thread.  The Celeron in my machine that I
    # benchmarked is basically a Core 2 Duo with a smaller cache, so
    # I’m going to assume that it could probably do about 1.5Mhash/s.
    # All common password-hashing algorithms (the ones mentioned
    # above, the others implemented in John, and bcrypt, but not
    # scrypt) use very little memory and, I believe, should scale on
    # GPUs comparably to the SHA-256 used in Bitcoin.

    # The same mining-hardware comparison says a Radeon 5870 card can
    # do 393.46 Mhash/s for US$350.

    print "But a modern GPU can crack about 250 times as fast,"
    print "so that same iterated MD5 would fall in %.1g GPU-years." % (t / 250)
    print

    # Suppose we depreciate the video card by Moore’s law,
    # i.e. halving in value every 18 months.  That's a loss of about
    # 0.13% in value every day; at US$350, that’s about 44¢ per day,
    # or US$160 per GPU-year.  If someone wanted your password as
    # quickly as possible, they could distribute the cracking job
    # across a network of millions of these cards.  The cards
    # additionally use about 200 watts of power, which at 16¢/kWh
    # works out to 77¢ per day.  If we assume an additional 20%
    # overhead, that’s US$1.45/day or US$529/GPU-year.
    cost_per_day = 1.45
    cost_per_crack = cost_per_day * 365 * t
    print "That GPU costs about US$%.2f per day to run in 2011," % cost_per_day
    print "so cracking the password would cost about US$%.1g." % cost_per_crack

def years(entropy, crypts_per_second):
    return float(2**entropy) / crypts_per_second / 86400 / 365.2422

if __name__ == '__main__':
    sys.exit(main(sys.argv))

implementing @Thomas Pornin solution

import M2Crypto
import string

def random_password(length=10):
    chars = string.ascii_uppercase + string.digits + string.ascii_lowercase
    password = ''
    for i in range(length):
        password += chars[ord(M2Crypto.m2.rand_bytes(1)) % len(chars)]
    return password