Find angle in degrees from one point to another in 2D space?
Solution 1:
I believe that the accepted answer does not correctly solve the problem for many people visiting this question. I am doing 2D simulations and the answer above does not solve my problem. Imagine the following circle:
$\hskip1.8in$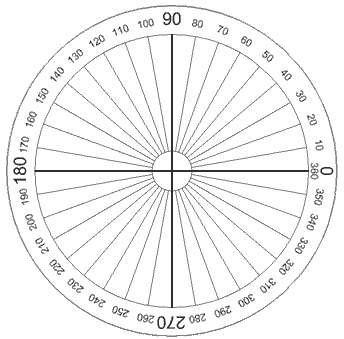
Assume that the middle of the circle is point A. Point B is at some angle from A according to the angles of the circle (so 0°) is right.
$\hskip2in$The atan2 function is what you need!
$$ atan2(y, x) $$ $\hskip3.2in$ Where
$$ y = y_B - y_A $$ $$ x = x_B - x_A $$
Read more about it here.
Solution 2:
From what I understood about your question, you want to find the angle between two points given their coordinates. In that case, first find the slope of the line using the slope formula: $$m=\dfrac{y_2-y_1}{x_2-x_1}$$ where $(x_1,y_1)$ and $(x_2,y_2)$ are coordinates on the line. Next, use this formula: $$\tan(\theta)=m$$ where $\theta$ is the angle. Therefore, the angle $\theta$ equals: $$\theta=\tan^{-1}(m)$$
Let's use the points $(0,10)$ and $(10,20)$ as an example (you mentioned it in your question). The slope is: $$m=\dfrac{10-20}{0-10}$$ $$m=\dfrac{-10}{-10}$$ $$m=1$$ Now we will find $\theta$. $$\tan(\theta)=1$$ $$\theta=\tan^{-1}(1)$$ $$\theta=45^\circ$$
Note: The $\tan(\theta)=m$ formula only gives the angle facing the positive $x$-axis (i.e. facing the "right"). So for a negative slope, you should get an angle that is greater than $90^\circ$.