What is limit superior and limit inferior?

I've looked at the Wikipedia article, but it seems like gibberish. The only thing I was able to pick out of it was the concept of infimum (greatest lower bound) and supremum (least upper bound), as I had learned them previously in an intro discrete math course.

The limit inferior of a sequence ($x_n$) is defined by

$\displaystyle\liminf_{n\to\infty}x_n := \lim_{n\to\infty}\Big(\inf_{m\geq n}x_m\Big)$

or

$\displaystyle\liminf_{n\to\infty}x_n := \sup_{n\geq 0}\,\inf_{m\geq n}x_m=\sup\{\,\inf\{\,x_m:m\geq n\,\}:n\geq 0\,\}.$

Similarly, the limit superior of ($x_n$) is defined by

$\displaystyle\limsup_{n\to\infty}x_n := \lim_{n\to\infty}\Big(\sup_{m\geq n}x_m\Big)$

or

$\displaystyle\limsup_{n\to\infty}x_n := \inf_{n\geq 0}\,\sup_{m\geq n}x_m=\inf\{\,\sup\{\,x_m:m\geq n\,\}:n\geq 0\,\}.$

Can anybody provide any examples of its use, and why it's used in that context?

I've found that some students have difficulty understanding the usual definitions of limit superior and inferior because these definitions combine the notions of limits, of suprema, and of infima, all of which the student may have learned only recently and not fully internalized. For such students, I like to give the following alternative definitions, equivalent to the usual ones but not containing the words "limit", "supremum", and "infimum". (Nor are there absolute values or visible $\varepsilon$'s.)

A number $t$ is the limit superior of a sequence $\langle a_n\rangle$ if the following two conditions are both satisfied:

• For every $s<t$ we have $s<a_n$ for infinitely many $n$'s.

• For every $s>t$ we have $s<a_n$ for only finitely many $n$'s (possibly none).

Similarly, a number $t$ is the limit inferior of a sequence $\langle a_n\rangle$ if the following two conditions are both satisfied:

• For every $s>t$ we have $s>a_n$ for infinitely many $n$'s.

• For every $s<t$ we have $s>a_n$ for only finitely many $n$'s (possibly none).

Two additional remarks may be useful:

1. The definition of lim inf is gotten from the definition of lim sup by simply reversing all inequalities.

2. The definitions can be easily extended to $\pm\infty$ in place of numbers $t$. Just adopt the convention that, even then, $s$ refers to actual numbers, all of which are $>-\infty$ and $<+\infty$.

A very prominent application of $\limsup$ is the Cauchy-Hadamard formula for the radius of convergence: Given a power series $\sum_{n=0}^\infty a_n x^n$, its radius f convergence $R$ can be obtained from $$\frac1R=\limsup_{n\to\infty}\sqrt[n]{|a_n|}.$$ Without going into details why that is so, let's ask:

• Why not the $\lim$? Because it may not even exist (e.g. if $a_n=1+(-1)^n$).

• Why not the $\sup$? Because a single large $|a_n|$ would then spoil the value whereas a single summand $a_nx^n$ does not influence the convergence.

Nevertheless, if $L:=\lim_{n\to\infty}\sqrt[n]{|a_n|}$ happens to exist, we see that the power series is dominated by $\sum |L' x|^n$ for any $L'>L$, and this converges (to $\frac1{1-|L'x|}$) provided $|L'x|<1$, and by suitable choice of $L'$ we obtain convergence whenever $|Lx|<1$. But if the limit does not exist, we must use the $\limsup$, so we have a sub-sequence converging to some $L$ and can choose the subsequence so large that all other terms $\sqrt[n]{|a_n|}$ are less than $L$. These small terms don't hurt the convergence if $|xL|<1$. And yet, since our subsequence has infinitely many terms, this is enough to spoil convergence when $|xL|>1$.

The most intuitive way I think is to try to understand what it is doing with a picture (credit Wikimedia Commons user Eigenjohnson):

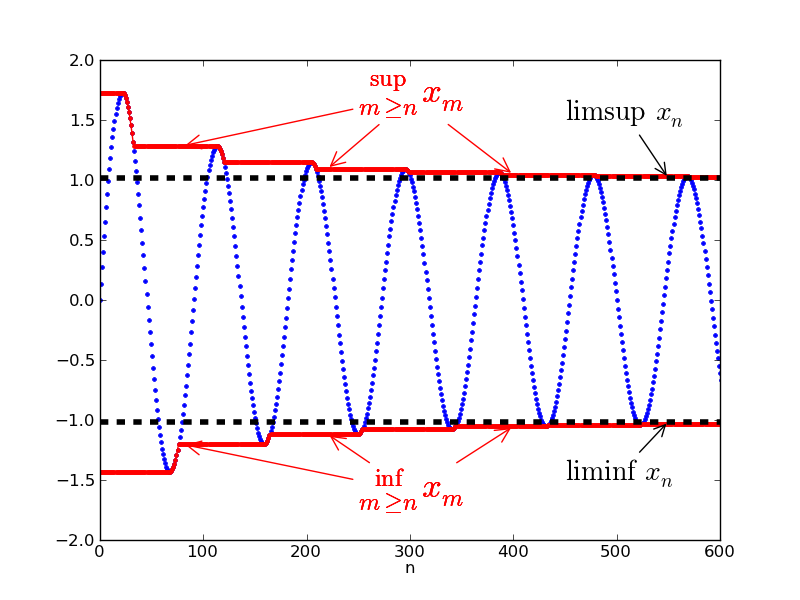
We know the maximum or minimum of a sequence may not exist, but the supremum and infimum always exist (if the sequence is bounded; if not we can consider the supremum/infimum in the extended real line as $\pm \infty$). However the supremum/infimum describes an upper/lower bound over the whole sequence, and so does not give us information about the tail of the sequence, or how the sequence eventually behaves. In the picture the supremum over the whole sequence $(x_n)$ is about 1.75 for early values in the sequence, but this doesn't tell us about later terms ($x_n$ for large $n$), which seem to have a supremum at 1.0.

$\liminf$ and $\limsup$ on the other hand tell us about the infimum and supremum as $n$ goes to infinity and we consider later and later $x_n$ terms. One definition (which I consider the most intuitive) is $$\limsup_{n \to \infty} x_n = \lim_{n \to \infty} \sup_{m \ge n} x_m$$

By the nature of this definition, we consider the supremum over the tail of the sequence of values $x_m$ or later, that is $(x_m)_{m \ge n}$, and by having the limit as $m \to \infty$ we consider later and later tails of the sequence. This captures the notion of best bounds of how the sequence eventually behaves for much later terms. Another nice thing about this definition is that $\limsup$ looks like $\lim$ of a $\sup$ and so we can remember what we're working with.

Another definition is $$\limsup_{n \to \infty} x_n = \sup \mathscr L$$

where $\mathscr L$ is the set of limit points of the sequence, that is all $l \in \mathbb R$ such that there exists a subsequence $(x_{n_k})$ that converges to $l$. (See Pedro Tamaroff's answer for more formal definition and explanation). This definition also captures the notion of how the sequence eventually behaves by considering all limit points, which by their nature consider how $x_{n_k}$ terms behave as $n$ goes to infinity. The proof that these two definitions are equivalent (see Two definitions of $\limsup$, Proof of equivalence of two definitions $\limsup$ and $\liminf$) sheds light on what exactly the definitions are doing.

A third characterization (in Andreas Blass's answer) is useful for proofs and says the following: if $l = \limsup_{n \to \infty} x_n$, then for all $\epsilon > 0$

• there exists $N \in \mathbb N$ such that for all $n \ge N$, $x_n \le l + \epsilon$, and
• $x_n \ge l - \epsilon$ for infinitely many $n \in \mathbb N$.

This characterization can be proved from the second definition by using the definition of limit and supremum (to prove, assume the contrary for each part and derive a contradiction. The first part uses Bolzano-Weierstrass theorem to find a convergent subsequence). Working through this definition and proving its equivalent to the second definition (with limit points) gives insight on what $\limsup$ means and the explicit use of $\epsilon$ makes it handy for proofs where we want explicit bounds to work with.

The following are answers of mine which use $\liminf$ and $\limsup$ [1] [2] [3] [4]

Maybe this helps.

DEF Given a sequence of real numbers $\langle a_n\rangle$, we say that $\ell \in \Bbb R^*=\Bbb R\cup\{+\infty,-\infty\}$ is a limit point of the sequence if there exists a subsequence $\langle a_{n_k}\rangle$ of $\langle a_n\rangle$ such that $$\lim_{k\to\infty}a_{n_k}=\ell $$

Now let's prove the

PROP Fix a sequence of real numbers $\langle a_n\rangle$, and define $$\mathscr L=\{x\in\Bbb R^*:x\text{ is a limit point of }\langle a_n\rangle\}$$ Then $\mathscr L$ is nonempty for any choice of $\langle a_n\rangle$.

P First suppose $\langle a_n\rangle$ is bounded. By Bolzano Weierstrass, there exists a convergent subsequence $\langle a_{n_k}\rangle$ of $\langle a_n\rangle$ such that $\lim\limits_{k\to\infty}a_{n_k}=\ell $ for some $\ell\in\Bbb R$. Thus $\ell\in\mathscr L$. Now assume $\langle a_n\rangle$ is unbounded. We can assume it is unbounded from above. Then, by definition, for each $k\in \Bbb N$ there exists $n_k$ such that $a_{n_k}\geq k$. It follows $\lim\limits_{k\to\infty}a_{n_k}=+\infty$, so $+\infty\in\mathscr L$.

Assume from now on the sequence is bounded.

DEF Let $\langle a_k\rangle$ be a sequence in $\Bbb R$. We define for each $n\in \Bbb N$ the associated sequences $$\overline{a_n}=\sup \langle a_k:k\geq n\rangle$$ $$\underline{a_n}=\inf \langle a_k:k\geq n\rangle$$ and subsequently the closed intervals $$A_n=\left[\underline{a_n},\overline{a_n}\right]$$

Observe that for each $n$, $$A_{n+1}\subseteq A_n$$

DEF For each sequence $\langle a_n\rangle$, define the intersection $$\bigcap_{n\in \Bbb N}A_n=[\zeta,\eta]$$This is nonempty courtesy of Cantor's intersection theorem.

Observe that $\zeta=\lim\limits_{n\to\infty} \underline{a_n}$ and $\eta=\lim\limits_{n\to\infty} \overline{a_n}$ are just the $\limsup$ and $\liminf$ of $\langle a_n\rangle $.

Prove

$1.$ If $\ell$ is a limit point of $\langle a_n\rangle $, then $\ell \in [\zeta,\eta]$. That is $\mathscr L\subseteq [\zeta,\eta]$.

$2.$ $\eta,\zeta$ are limit points of $\langle a_n\rangle $, thus conclude that $\eta,\zeta$ are the smallest and largest limit points of $\langle a_n\rangle $. Thus $\zeta=\sup\mathscr L=\max \mathscr L\; ,\; \eta=\inf\mathscr L=\min \mathscr L$.

$3.$ Observe that if $\zeta=\eta$, the interval degenerates to a single point $p=\zeta=\eta$, which means that the trivial subsequence $\langle a_n\rangle $ converges to $p=\zeta=\eta$. Conversely, if $\lim\limits_{n\to\infty} a_n=p$, all subsequences converge to $p$, so the interval $[\zeta,\eta]$ degenerates to the single point $p=\eta=\zeta$.

NOTE If the sequence is unbounded from above (resp. below) then $$\limsup_{n\to\infty}a_n=+\infty\;\;\left( \liminf_{n\to\infty}a_n=-\infty\right)$$