A geometric look at $\frac{1}{a}+\frac{1}{b}=\frac{1}{c}$?

Solution 1:

If you have two poles of length $a$ and $b$, and string wire from the top of one pole to the bottom of the other, and vice versa, the height $c$ at which the wires intersect will be given by half the harmonic mean of the height of the two poles, $\displaystyle \dfrac{1}{c} = \dfrac{1}{a} + \dfrac{1}{b}$, no matter how far apart they are. This can be easily shown using similar triangles.

I can also think of one more place where the harmonic mean is commonly found in a geometric context: Given a right triangle with legs $a$, $b$, the squared height of the altitude to the hypotenuse is given by half the harmonic mean of the squared lengths. Wikipedia provides a handy diagram so I'll just quickly write it out:

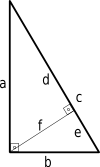
(Here $A$, $B$, $C$ are the angles opposite the lowercase sides, as is usual, and $P$ is the point where the altitude intersects the hypotenuse.) Then, since $\bigtriangleup ABC \; \sim \; \; \bigtriangleup CBP \;$,

$$\dfrac{a}{f} = \dfrac{c}{b} \Rightarrow \dfrac{a^2}{f^2} = \dfrac{c^2}{b^2} = \dfrac{a^2 + b^2}{b^2}$$

So, by cross-multiplying we get,

$$\dfrac{1}{f^2} = \dfrac{a^2 + b^2}{a^2b^2} = \dfrac{1}{a^2} + \dfrac{1}{b^2}$$

half the harmonic mean of the squared lengths.

Solution 2:

Given three circles of areas $a\geq b\geq c >0$, they can be put in a position such that they are tangent to each other and to a straight line if and only if $$ \frac{1}{c} = \frac{1}{a} + \frac{1}{b}. $$

Note that this a special case of Descartes' theorem.

Solution 3:

Not necessarily geometric, but if $a$ and $b$ are electrical resistances placed in parallel, then their combined resistance is $c$.

Solution 4:

You find this kind of “addition” happening frequently. For instance, if you have lenses of focal length $a$ and $b$ and put them together, the combined focal length is $c$. What's happening in this case is that the “strength” of the first lens is $1/a$, of the second is $1/b$, and the strengths add.

Another example from optics is that if you have a lens of focal length $c$ and place something a distance of $a$ in front of it, the image forms at a distance of $b$ behind the lens.