Different ways to come up with $1+2+3+\cdots +n=\frac{n(n+1)}{2}$

I am trying to compile a list of the different ways to come up with the closed form for the sum in the title. So far I have the famous Gauss story, the argument by counting doubletons, and using generating functions. Is there any other (significantly) different way to discover the closed form?

To clarify, Gauss's method was to take $1+2+3+\dots+n$, write it backwards, and add it up.

You have an education tag so perhaps you're looking for a less rigorous proof which might just make sense to students.

If you have the consecutive numbers $1,2,3,4,...,n$ in order then the average of the numbers is in the middle, that's the smallest number plus the largest divided by $2$.

$\text{average} = \frac{n+1}{2}$

Of course the main definition of the average is the sum of all the numbers divided by how many numbers there are.

$\text{average} = \frac{1+2+3+4+...+n}{n}$

Equating these two:

$\frac{1+2+3+4+...+n}{n} = \frac{n+1}{2}$

And therefore

$1+2+3+4+...+n = n\frac{n+1}{2}$

One significantly different method is to bulldozer through using the Euler-Maclaurin formula:

$$\sum_{k=1}^nk=\int_0^nx\ dx+\frac12n+c=\frac12n^2+\frac12x+c$$

for some constant $c$. Plugging in $n=1$ reveals that $c=0$, so

$$\sum_{k=1}^nk=\frac12n^2+\frac12n$$

One can also try the hockey-stick identity:

$$\sum_{k=1}^nk=\sum_{k=1}^n\binom k1=\binom{n+1}2=\frac{n(n+1)}{2!}$$

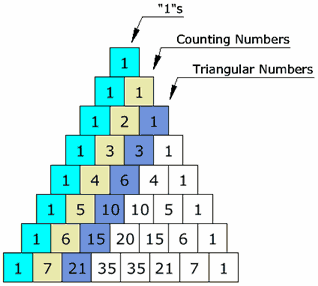
(poor ones get a lame name) As you can see, each diagonal is the sum of the previous due to how Pascal's triangle is made.

Many more methods to computing this sum may be found in one of my favorite questions:

Methods to compute $\sum_{k=1}^nk^p$ without Faulhaber's formula

I want to add this proof because is very interesting, but I want to be clear stating that the merit is of the user @SimplyBeautifulArt in this post:

If you knew of the geometric series, you would know that

$$\frac{1-r^{n+1}}{1-r}=1+r+r^2+r^3+\dots+r^n$$

If we differentiate both sides, we have

$$\frac{nr^{n+2}-(n+1)r^{n+1}+r}{(1-r)^2}=1+2r+3r^2+\dots+nr^{n-1}$$

Letting $r\to1$ and applying L'Hospital's rule on the fraction, we end up with

$$\frac{n(n+1)}2=1+2+3+\dots+n$$