Are Exercises the Surest Path to Enlightenment? [closed]

Solution 1:

I have a nagging fear that I might be missing part of the puzzle by focusing so much on the exercises

An argument can be made that "good" textbooks are designed in a way that exercises and theory go hand-in-hand. The only difference is that text is supposed to be the passive form, i.e. "This is x", and exercises are meant to flex your brain, "Is this x?". Exercises are often a part of a book/course, in a way that if you skip them then you haven't really completed the book/course.

Now let's try to understand the role of exercises a little better so that we could talk intelligently about substitutes for exercises.

Since this question is about learning, consider the levels in Bloom's Taxonomy

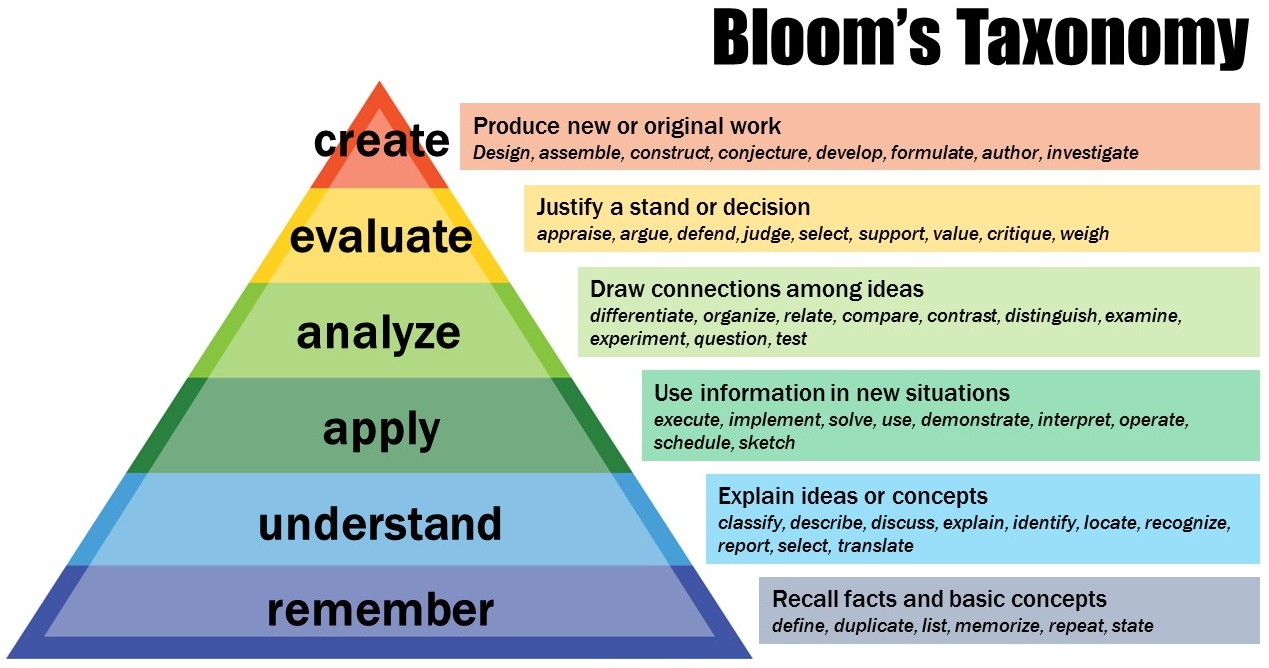
I feel that exercises are a versatile tool in mathematics because they can be made to target the levels of evaluation, analysis, application, and understanding (the most basic of problems)

After you do exercises, you'll find that the role they play is that they concretize the levels below it in your head.

As an example – in order to do an understanding problem, you'll have to refer to the theorems, properties and propositions which falls in the remembering domain. And similarly, in order to apply math in a new situation, you'll first have to understand the mathematics that's going on behind the scenes. And so on, each level depends on mastery of the level below it.

You'll find that if you keep on reading new things without having a concrete mastery of the topics it depends upon, you'll get lost.

"Did the 'masters' of modern mathematics (early 1900's to today) primarily emphasize exercises in their education or did they achieve their mastery through some other means?

I don't have any historical information, but now that we've discerned the role of exercises, maybe if someone is able to concretize their knowledge in some other way, then they could get away with not doing exercises because it won't really be of any use to them.

Mathematics gradually builds up on the topics previously studied. Exercises help you concretize the topics you're studying so you could depend on your understanding of the topic when you set out to study the next one. It isn't exercises which are important, but this effect - which may be fulfilled by some other ways as well.

Solution 2:

My answer is YES. I shall start with some generalisation.

In every field, you are Master if you are capable of doing things on the ground level (in real world). There is nothing which you can't understand, but there are a lot of things which you can't learn. Because you understand something when you study it, observe it, but you learn something when you apply the knowledge you have about that thing in reality.

We study so that we can apply the knowledge which we are gaining . Application is everything and knowledge can be applied only when you now When to apply/ Where to apply and How to apply. How can someone get the answers of when to apply/where to apply and how to apply?? It is easy, just apply. If you want to know how mango tastes, you will have to eat it.

In mathematics, problems are the objects on which you can apply your knowledge. So, doing problem/exercises is finding application, and finding application is ultimately learning.