If $f\!: X\simeq Y$, then $X\!\cup_\varphi\!\mathbb{B}^k \simeq Y\!\cup_{f\circ\varphi}\!\mathbb{B}^k$.

How can I prove that if two spaces $X$ and $Y$ are homotopy equivalent, then the corresponding spaces obtained by gluing a $k$-cell are also equivalent?

In detail, if $\varphi\!:\mathbb{S}^{k-1}\!\rightarrow\!X$ is a continuous map and $f\!:X\!\rightarrow\!Y$ is a homotopy equivalence, then $X\!\cup_\varphi\!\mathbb{B}^k$ and $Y\!\cup_{f\circ\varphi}\!\mathbb{B}^k$ are homotopy equivalent.

This is motivated by Shastri's Elements of Differential Topology, p.226, Corollary 8.3.4, Proof (i): .

My attempt: We extend $f$ to a map $\overline{f}\!:X_i\!\cup_\varphi\!\mathbb{B}^k \longrightarrow Y\!\cup_{f\circ\varphi}\!\mathbb{B}^k$ with the identity on $\mathbb{\mathring{B}}^k$. Then $\overline{f}$ is continuous: for every convergent sequence $\mathbb{\mathring{B}}^k\!\ni a_n\!\longrightarrow a\!\in\!\partial\mathbb{B}^k$ and $\varphi(a)\!=\!x\!\in\!X$, there holds $\mathbb{\mathring{B}}^k\!\ni \overline{f}(a_n)\!=\! a_n\!\longrightarrow a\!\in\!\partial\mathbb{B}^k$ and $f\!\circ\!\varphi(a)\!=\! \overline{f}(x)\!\in\!Y$, hence $\overline{f}(\lim_na_n)\!=\!\lim_n\overline{f}(a_n)$. Similarly, we extend the homotopy inverse $f'$ of $f$ to a map $\overline{f'}\!:Y_i\!\cup_{f\circ\varphi}\!\mathbb{B}^k \!\longrightarrow\! X\!\cup_{\varphi}\!\mathbb{B}^k$ with the identity on $\mathbb{\mathring{B}}^k$. Then $\overline{f'}$ is also continuous: for every convergent sequence $\mathbb{\mathring{B}}^k\!\ni a_n\!\longrightarrow a\!\in\!\partial\mathbb{B}^k$ and $f\!\circ\!\varphi(a)\!=\!y\!\in\!Y$, we have $\mathbb{\mathring{B}}^k\!\ni \overline{f'}(a_n)\!=\! a_n\!\longrightarrow a\!\in\!\partial\mathbb{B}^k$ and $\varphi(a) \overset{???}{=} \overline{f'}\!\circ\!f\!\circ\!\varphi(a) \!=\! \overline{f'}(y)\!\in\!X$, hence $\overline{f'}(\lim_na_n)\!=\!\lim_n\overline{f'}(a_n)$. Then we extend the homotopy $h\!:f'\!\circ\!f\simeq\mathrm{id}_X$ to a map $\overline{h}\!: (X_i\!\cup_\varphi\!\mathbb{B}^k)\!\times\!\mathbb{I} \longrightarrow X_i\!\cup_\varphi\!\mathbb{B}^k$ with the identity on $\mathbb{\mathring{B}}^k\!\times\!\mathbb{I}$. Similarly, we extend the homotopy $h'\!:f\!\circ\!f'\simeq\mathrm{id}_Y$.

Edit: From Milnor's Morse Theory, p. 21:

Question 1: In lemma 3.6, how do I define $l$? I don't think the following works: $$\begin{array}{l} l(x)=x &;\; x\!\in\!X\\ l(tu)=2tu &;\; t\!\in\!{\textstyle[0,\frac{1}{2}]}, u\!\in\!S^{k-1}\\ l(tu)=\varphi_{2t-1}(u) & ;\; t\!\in\!{\textstyle[\frac{1}{2},1]}, u\!\in\!S^{k-1}. \end{array}$$ Furthermore, what are then the homotopies between $kl$ and $lk$?

Edit: This $l$ turns out to be ok. Then we have $$k\!\circ\!l\!=\!\! \begin{cases} \;\:x \mapsto x & ;\; x\!\in\!X\\ tu \mapsto 4tu & ;\; t\!\in\![0,\frac{1}{4}], u\!\in\!\mathbb{S}^{k-1}\\ tu \mapsto \varphi_{2-4t}(u) & ;\; t\!\in\![\frac{1}{4},\frac{1}{2}], u\!\in\!\mathbb{S}^{k-1}\\ tu \mapsto \varphi_{2t-1}(u) & ;\; t\!\in\![\frac{1}{2},1], u\!\in\!\mathbb{S}^{k-1} \end{cases}$$ and $$l\circ\!k\!=\!\! \begin{cases} \;\:x \mapsto x & ;\; x\!\in\!X\\ tu \mapsto 4tu & ;\; t\!\in\![0,\frac{1}{4}], u\!\in\!\mathbb{S}^{k-1}\\ tu \mapsto \varphi_{4t-1}(u) & ;\; t\!\in\![\frac{1}{4},\frac{1}{2}], u\!\in\!\mathbb{S}^{k-1}\\ tu \mapsto \varphi_{2-2t}(u) & ;\; t\!\in\![\frac{1}{2},1], u\!\in\!\mathbb{S}^{k-1} \end{cases}.$$ The desired homotopies are then (where $s$ is the time parameter) $$\begin{array}{ c @{\hspace{2pt}} l} \alpha\!\circ\!\beta\simeq \mathrm{id}_{X\cup_{\varphi_1}\mathbb{B}^k} & \;\;u\!\in\!\mathbb{S}^{k-1}\\ x & ;\; x\!\in\!X\\ (4\!-\!3s)tu & ;\; t\!\in\![0,\frac{1}{4}] \\[1pt] (1\!+\!s(t\!-\!1))\varphi_{4t(s-1)+2-s}(u) & ;\; t\!\in\![\frac{1}{4},\frac{1}{2}]\\[1pt] (1\!+\!s(t\!-\!1))\varphi_{2t(1-s)+2s-1}(u) & ;\; t\!\in\![\frac{1}{2},1] \end{array}$$ and $$\begin{array}{c @{\hspace{2pt}} l} \beta\circ\!\alpha\simeq \mathrm{id}_{X\cup_{\varphi_0}\mathbb{B}^k} & \;\;u\!\in\!\mathbb{S}^{k-1}\\ x & ;\; x\!\in\!X\\ (4\!-\!3s)tu & ;\; t\!\in\![0,\frac{1}{4}]\\[1pt] (1\!+\!s(t\!-\!1))\varphi_{(4t-1)(1-s)}(u) & ;\; t\!\in\![\frac{1}{4},\frac{1}{2}]\\[1pt] (1\!+\!s(t\!-\!1))\varphi_{2(1-t)(1-s)}(u) & ;\; t\!\in\![\frac{1}{2},1] \end{array}. $$

Question 2: In lemma 3.7, how can I see that $G$ has a left inverse?

Solution 1:

This result is a special case of a Gluing Theorem for homotopy equivalences, which can be expressed as follows. Suppose given the following commutative cubical diagram

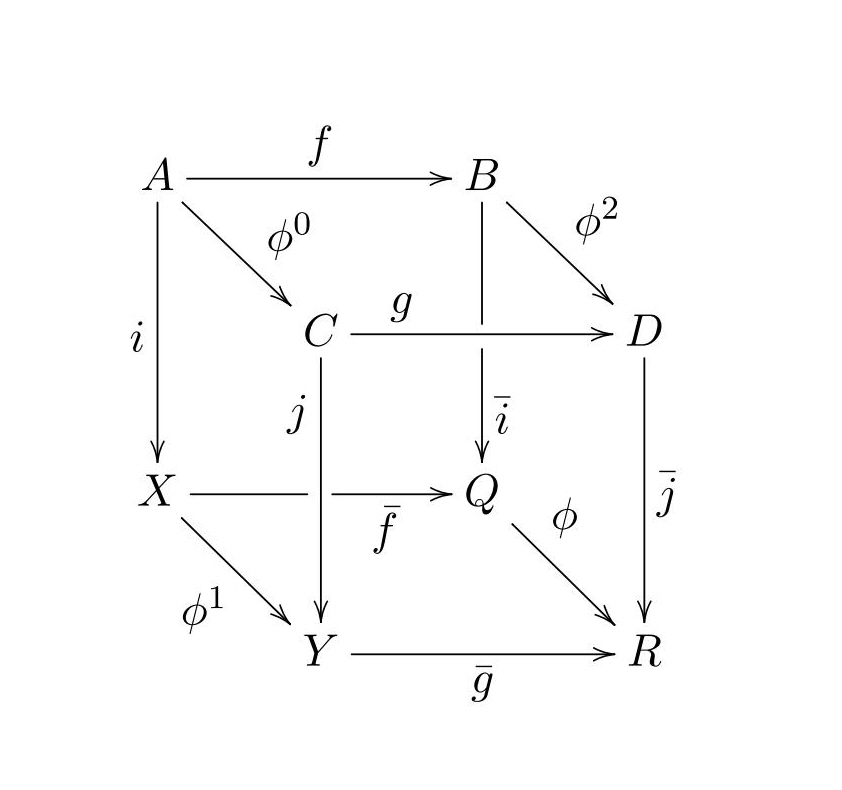
in which the back and front faces are pushouts and $i,j$ are closed cofibrations. Suppose that $\phi^i$ are homotopy equivalences for $i=0,1,2$. Then the map $\phi: Q \to R$, which is of course determined by the rest of the diagram, is also a homotopy equivalence.

This result is 7.5.7 of my book Topology and Groupoids and in fact was first published, but without the cubical diagram, in the 1968 edition called "Elements of Modern Topology". The proof here also gives good control of the homotopies.

Later: The result was found by starting with the standard result that a homotopy equivalence $f: Y \to Z$ of topological spaces induces an isomorphism of homotopy groups, and then generalising by replacing $(S^n,x)$ by a pair $(X,A)$ for which $A \to X$ is a closed cofibration. This led to the possibility of gluing homotopy equivalences of parts of a union where the equivalences agreed on the intersection $A$.

This theorem has also been proved in the context of model categories for homotopy theory.

Aug 30: Leon asked me why $G$ in Milnor's proof has a left homotopy inverse. I think the idea is the same as for $F$ but you use the composition $$Y \cup _{f \phi} e^n \to X \cup_{gf\phi} e^n \to Y \cup_{fgf\phi}e^n$$ and then use the homotopy $fg \simeq 1$.

I have an objection to Milnor's proof in that the homotopy $q_{\tau}$ is just written down; that seems ad hoc, and I would prefer more justification. Part of the motivation of my exposition was to give reasons for the existence of homotopies, as I found some of the original papers hard to follow.

One categorical fact behind this result is that if $a,b,c$ are morphisms in a category and $cb, ba$ are defined and are isomorphisms, then $a,b,c$ are isomorphisms. But when you examine the proof of this, and apply it to the problem asked, you find that some of the homotopies involved in the final homotopy equivalence are not straight combinations of the original homotopies, but are kinds of ``conjugates''.

Hope that helps.

April 30, 2020 You could also look at work on strong homotopy equivalences by Vogt, and by C. B Spencer, Cahiers de Topologie et Géométrie Différentielle Catégoriques, Volume 18 (1977) no. 4, p. 409-429. cf here.