Roulette Selection in Genetic Algorithms

Can anyone provide some pseudo code for a roulette selection function? How would I implement this:

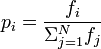
I don't really understand how to read this math notation. I never took any probability or statistics.

It's been a few years since i've done this myself, however the following pseudo code was found easily enough on google.

for all members of population
    sum += fitness of this individual
end for

for all members of population
    probability = sum of probabilities + (fitness / sum)
    sum of probabilities += probability
end for

loop until new population is full
    do this twice
        number = Random between 0 and 1
        for all members of population
            if number > probability but less than next probability 
                then you have been selected
        end for
    end
    create offspring
end loop

The site where this came from can be found here if you need further details.

Lots of correct solutions already, but I think this code is clearer.

def select(fs):
    p = random.uniform(0, sum(fs))
    for i, f in enumerate(fs):
        if p <= 0:
            break
        p -= f
    return i

In addition, if you accumulate the fs, you can produce a more efficient solution.

cfs = [sum(fs[:i+1]) for i in xrange(len(fs))]

def select(cfs):
    return bisect.bisect_left(cfs, random.uniform(0, cfs[-1]))

This is both faster and it's extremely concise code. STL in C++ has a similar bisection algorithm available if that's the language you're using.

The pseudocode posted contained some unclear elements, and it adds the complexity of generating offspring in stead of performing pure selection. Here is a simple python implementation of that pseudocode:

def roulette_select(population, fitnesses, num):
    """ Roulette selection, implemented according to:
        <http://stackoverflow.com/questions/177271/roulette
        -selection-in-genetic-algorithms/177278#177278>
    """
    total_fitness = float(sum(fitnesses))
    rel_fitness = [f/total_fitness for f in fitnesses]
    # Generate probability intervals for each individual
    probs = [sum(rel_fitness[:i+1]) for i in range(len(rel_fitness))]
    # Draw new population
    new_population = []
    for n in xrange(num):
        r = rand()
        for (i, individual) in enumerate(population):
            if r <= probs[i]:
                new_population.append(individual)
                break
    return new_population

This is called roulette-wheel selection via stochastic acceptance:

/// \param[in] f_max maximum fitness of the population
///
/// \return index of the selected individual
///
/// \note Assuming positive fitness. Greater is better.

unsigned rw_selection(double f_max)
{
  for (;;)
  {
    // Select randomly one of the individuals
    unsigned i(random_individual());

    // The selection is accepted with probability fitness(i) / f_max
    if (uniform_random_01() < fitness(i) / f_max)
      return i;
  }   
}

The average number of attempts needed for a single selection is:

τ = f_max / avg(f)

• f_max is the maximum fitness of the population
• avg(f) is the average fitness

τ doesn't depend explicitly on the number of individual in the population (N), but the ratio can change with N.

However in many application (where the fitness remains bounded and the average fitness doesn't diminish to 0 for increasing N) τ doesn't increase unboundedly with N and thus a typical complexity of this algorithm is O(1) (roulette wheel selection using search algorithms has O(N) or O(log N) complexity).

The probability distribution of this procedure is indeed the same as in the classical roulette-wheel selection.

For further details see:

• Roulette-wheel selection via stochastic acceptance (Adam Liposki, Dorota Lipowska - 2011)

Here is some code in C :

// Find the sum of fitnesses. The function fitness(i) should 
//return the fitness value   for member i**

float sumFitness = 0.0f;
for (int i=0; i < nmembers; i++)
    sumFitness += fitness(i);

// Get a floating point number in the interval 0.0 ... sumFitness**
float randomNumber = (float(rand() % 10000) / 9999.0f) * sumFitness;

// Translate this number to the corresponding member**
int memberID=0;
float partialSum=0.0f;

while (randomNumber > partialSum)
{
   partialSum += fitness(memberID);
   memberID++;
} 

**// We have just found the member of the population using the roulette algorithm**
**// It is stored in the "memberID" variable**
**// Repeat this procedure as many times to find random members of the population**