Finding out nth fibonacci number for very large 'n'
I was wondering about how can one find the nth term of fibonacci sequence for a very large value of n say, 1000000. Using the grade-school recurrence equation fib(n)=fib(n-1)+fib(n-2), it takes 2-3 min to find the 50th term!
After googling, I came to know about Binet's formula but it is not appropriate for values of n>79 as it is said here
Is there an algorithm to do so just like we have for finding prime numbers?
You can use the matrix exponentiation method (linear recurrence method). You can find detailed explanation and procedure in this blog. Run time is O(log n).
I don't think there is a better way of doing this.
You can save a lot time by use of memoization. For example, compare the following two versions (in JavaScript):
Version 1: normal recursion
var fib = function(n) {
return n < 2 ? n : fib(n - 1) + fib(n - 2);
};
Version 2: memoization
A. take use of underscore library
var fib2 = _.memoize(function(n) {
return n < 2 ? n : fib2(n - 1) + fib2(n - 2);
});
B. library-free
var fib3 = (function(){
var memo = {};
return function(n) {
if (memo[n]) {return memo[n];}
return memo[n] = (n <= 2) ? 1 : fib3(n-2) + fib3(n-1);
};
})();
The first version takes over 3 minutes for n = 50 (on Chrome), while the second only takes less than 5ms! You can check this in the jsFiddle.
It's not that surprising if we know version 1's time complexity is exponential (O(2N/2)), while version 2's is linear (O(N)).
Version 3: matrix multiplication
Furthermore, we can even cut down the time complexity to O(log(N)) by computing the multiplication of N matrices.
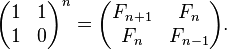
where Fn denotes the nth term of Fibonacci sequence.
I agree with Wayne Rooney's answer that the optimal solution will complete in O(log n) steps, however the overall run-time complexity will depend upon the complexity of the multiplication algorithm used. Using Karatsuba Multiplication, for example, the overall run-time complexity would be O(nlog23) ≈ O(n1.585).1
However, matrix exponentiation isn't necessarily the best way to go about it. As a developer at Project Nayuki has noticed, matrix exponentiation carries with it redundant calculations, which can be removed. From the author's description:
Given Fk and Fk+1, we can calculate these:
Note that this requires only 3 BigInt-to-BigInt multiplications per split, rather than 8 as matrix exponentiation would.
We can still do slightly better than this, though. One of the most elegant Fibonacci identities is related to the Lucas Numbers:
where Ln is the nth Lucas Number. This identity can be further generalized as:
There's a few more-or-less equivalent ways to proceed recursively, but the most logical seems to be on Fn and Ln. Further identities used in the implementation below can either be found or derived from the identities listed for Lucas Sequences:
Proceeding in this way requires only two BigInt-to-BigInt multiplications per split, and only one for the final result. This is about 20% faster than the code provided by Project Nayuki (test script). Note: the original source has been modified (improved) slightly to allow a fair comparison.
def fibonacci(n):
def fib_inner(n):
'''Returns F[n] and L[n]'''
if n == 0:
return 0, 2
u, v = fib_inner(n >> 1)
q = (n & 2) - 1
u, v = u * v, v * v + 2*q
if (n & 1):
u1 = (u + v) >> 1
return u1, 2*u + u1
return u, v
u, v = fib_inner(n >> 1)
if (n & 1):
q = (n & 2) - 1
u1 = (u + v) >> 1
return v * u1 + q
return u * v
Update
A greybeard points out, the above result has already been improved upon by Takahashi (2000)2, by noting that BigInt squaring is generally (and specifically for the Schönhage-Strassen algorithm) less computationally expensive than BigInt multiplication. The author suggestions an iteration, splitting on Fn and Ln, using the following identities:
Iterating in this way will require two BigInt squares per split, rather than a BigInt square and a BigInt multiplication as above. As expected, the run-time is measurably faster than the above implementation for very large n, but is somewhat slower for small values (n < 25000).
However, this can be improved upon slightly as well. The author claims that, "It is known that the Product of Lucas Numbers algorithm uses the fewest bit operations to compute the Fibonacci number Fn." The author then elects to adapt the Product of Lucas Numbers algorithm, which at the time was the fastest known, splitting on Fn and Ln. Note, however, that Ln is only ever used in the computation of Fn+1. This seems a somewhat wasteful, if one considers the following identities:
where the first is taken directly from Takahashi, the second is a result of the matrix exponentiation method (also noted by Nayuki), and the third is the result of adding the previous two. This allows an obvious split on Fn and Fn+1. The result requires one less BigInt addition, and, importantly, one less division by 2 for even n; for odd n the benefit is doubled. In practice this is signifcantly faster than the method proposed by Takahashi for small n (10-15% faster), and marginally faster for very large n (test script).
def fibonacci(n):
def fib_inner(n):
'''Returns F[n] and F[n+1]'''
if n == 0:
return 0, 1
u, v = fib_inner(n >> 1)
q = (n & 2) - 1
u *= u
v *= v
if (n & 1):
return u + v, 3*v - 2*(u - q)
return 2*(v + q) - 3*u, u + v
u, v = fib_inner(n >> 1)
# L[m]
l = 2*v - u
if (n & 1):
q = (n & 2) - 1
return v * l + q
return u * l
Update 2
Since originally posting, I've improved upon the previous result slightly as well. Aside from the two BigInt squares, splitting on Fn and Fn+1 also has an overhead of three BigInt additions and two small constant multiplications per split. This overhead can be eliminated almost entirely by splitting on Ln and Ln+1 instead:
Splitting in this way requires two BigInt squares as before, but only a single BigInt addition. These values need to be related back to the corresponding Fibonacci number, though. Fortunately, this can be achieved with a single division by 5:
Because the quotient is known to be integer, an exact division method such as GMP's mpz_divexact_ui can be used. Unrolling the outermost split allows us to then compute the final value with a single multiplication:
As implemented in Python, this is noticably faster than the previous implementation for small n (5-10% faster) and marginally faster for very large n (test script).
def fibonacci(n):
def fib_inner(n):
'''Returns L[n] and L[n+1]'''
if n == 0:
return mpz(2), mpz(1)
m = n >> 1
u, v = fib_inner(m)
q = (2, -2)[m & 1]
u = u * u - q
v = v * v + q
if (n & 1):
return v - u, v
return u, v - u
m = n >> 1
u, v = fib_inner(m)
# F[m]
f = (2*v - u) / 5
if (n & 1):
q = (n & 2) - 1
return v * f - q
return u * f
1 It can be seen that the number of digits (or bits) of Fn ~ O(n) as:
The runtime complexity using Karatsuba Multiplication can then be calculated as:
2 Takahashi, D. (2000), "A fast algorithm for computing large Fibonacci numbers" (PDF), Information Processing Letters 75, pp. 243–246.